Для любого алгоритма с восхождением к вершине, который никогда не выполняет движения "вниз по склону", к состояниям с более низкой оценкой (или более высокой стоимостью), гарантируется, что он окажется неполным, поскольку такой алгоритм всегда способен зайти в тупик, достигнув локального максимума. В отличие от этого алгоритм с чисто случайным блужданием (т.е. с перемещением к преемнику, выбираемому на равных правах случайным образом из множества преемников) является полным, но чрезвычайно неэффективным. Поэтому представляется разумной попытка скомбинировать каким-то образом восхождение к вершине со случайным блужданием, что позволит обеспечить и эффективность, и полноту. Алгоритмом такого типа является алгоритм с эмуляцией отжига. В металлургии отжигом называется процесс, применяемый для отпуска металла и стекла путем нагревания этих материалов до высокой температуры, а затем постепенного охлаждения, что позволяет перевести обрабатываемый материал в низкоэнергетическое кристаллическое состояние. Чтобы понять суть эмуляции отжига, переведем наше внимание с восхождения к вершине на градиентный спуск (т.е. минимизацию стоимости) и представим себе, что наше задание — загнать теннисный шарик в самую глубокую лунку на неровной поверхности. Если бы мы просто позволили шарику катиться по этой поверхности, то он застрял бы в одном из локальных минимумов. А встряхивая поверхность, можно вытолкнуть шарик из локального минимума. Весь секрет состоит в том, что поверхность нужно трясти достаточно сильно, чтобы шарик можно было вытолкнуть из локальных минимумов, но не настолько сильно, чтобы он вылетел из глобального минимума. Процесс поиска решения с эмуляцией отжига заключается в том, что вначале происходит интенсивное встряхивание (аналогичное нагреву до высокой температуры), после чего интенсивность встряхивания постепенно уменьшается (что можно сравнить с понижением температуры).

Самый внутренний цикл алгоритма с эмуляцией отжига (листинг 4.3) полностью аналогичен циклу алгоритма с восхождением к вершине, но в нем вместо наилучшего хода выполняется случайно выбранный ход. Если этот ход улучшает ситуацию, то всегда принимается. В противном случае алгоритм принимает данный ход с некоторой вероятностью, меньшей 1. Эта вероятность уменьшается экспоненциально с "ухудшением" хода—в зависимости от величины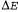; на которую ухудшается его оценка. Кроме того, вероятность уменьшается по мере снижения "температуры" т. "плохие" ходы скорее всего могут быть разрешены в начале, когда температура высока, но становятся менее вероятными по мере снижения Т. Можно доказать, что если в графике schedule предусмотрено достаточно медленное снижение Т, то данный алгоритм позволяет найти глобальный оптимум с вероятностью, приближающейся к 1.