Предположим, что [ true, true, false, true, true] — последовательность истинностных значений с результатами наблюдений за появлением директора с зонтиком, которые проводил охранник в течение первых пяти дней своей работы. Какая последовательность состояний погоды может стать наиболее вероятным объяснением для этих данных? Означает ли отсутствие зонтика в день 3, что не было дождя или директор забыл его взять? А если в день 3 не было дождя, то, возможно, дождь не шел и в день 4 (поскольку погода обычно является устойчивой), однако директор захватил с собой зонтик просто на всякий случай. В целом существуютвозможных последовательностей состояний погоды, которые могут быть приняты в качестве объяснения. Но есть ли способ найти наиболее вероятную из этих последовательностей, не перебирая их все?

Один из подходов, который может быть опробован, состоит в использовании следующей процедуры с линейными затратами времени: с помощью алгоритма сглаживания найти распределения апостериорных вероятностей погоды на каждом временном интервале; после этого составить последовательность, используя на каждом этапе наиболее вероятное состояние погоды, соответствующее этим апостериорным вероятностям. Но такой подход должен вызвать у читателя сомнения, поскольку апостериорные вероятности, вычисленные с помощью сглаживания, представляют собой распределения вероятностей для отдельных временнь/х интервалов, тогда как, чтобы найти наиболее вероятную последовательность, необходимо рассматривать совместные вероятности по всем временным интервалам. Соответствующие результаты фактически могут оказаться довольно различными.

Тем не менее алгоритм поиска наиболее вероятной последовательности с линейными затратами времени существует, но чтобы его найти, необходимо продумать все обстоятельства немного более тщательно. Алгоритм должен быть основан на том же свойстве марковости (неизменности порядка марковской цепи), которое позволило создать эффективные алгоритмы фильтрации и сглаживания. Проще всего можно подойти к решению этой задачи, рассматривая каждую последовательность как путь в графе, узлами которого являются возможные состояния на каждом временном интервале. Такой граф показан для мира задачи с зонтиком на рис. 15.4, а. Теперь рассмотрим задачу поиска наиболее вероятного пути через этот граф, где значение правдоподобия любого пути представляет собой произведение вероятностей перехода вдоль этого пути и вероятностей конкретных наблюдений в каждом состоянии. В частности, сосредоточимся на тех путях, которые достигают состояния . Ввиду наличия свойства марковости можно прийти к заключению, что наиболее вероятный путь к состоянию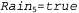состоит из наиболее вероятного пути к некоторому состоянию, достигнутому во время 4, за которым следует переход в состояние Rain5= true, а состоянием во время 4, которое станет частью пути к состоянию Rain5=true, является именно то состояние, которое максимизирует значение правдоподобия этого пути. Иными словами, существует рекурсивная связь между наиболее вероятными путями в каждое состояниеи наиболее вероятными путями в каждое состояние xt. Эту связь можно записать в виде уравнения, соединяющего вероятности путей, следующим образом:

(15.9)