Уравнение 15.9 идентично уравнению фильтрации 15.3, за исключением описанных ниже отличий.

1.    Прямое сообщение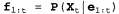заменяется следующим сообщением, т.е. вероятностями наиболее правдоподобного пути в каждое состояние: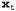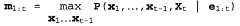

2.    Суммирование по переменнымв уравнении 15.3 заменяется максимизацией по переменным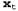в уравнении 15.9.

Таким образом, алгоритм вычисления наиболее вероятной последовательности аналогичен алгоритму фильтрации: он проходит в прямом направлении вдоль последовательности, вычисляя сообщение m на каждом временном интервале с помощью уравнения 15.9. Ход этих вычислений показан на рис. 15.4, б. В конечном итоге этот алгоритм позволяет получить вероятность наиболее правдоподобной последовательности, достигающей каждого из заключительных состояний. Поэтому с его помощью можно легко выбрать последовательность, которая является наиболее правдоподобной среди всех прочих (соответствующие ей состояния обозначены на рисунке жирными контурами). Для того чтобы иметь возможность определить фактически наблюдаемую последовательность, а не просто вычислить ее вероятность, в этом алгоритме необходимо также сопровождать указатели от каждого состояния обратно к наилучшему состоянию, приведшему к нему (эти указатели показаны на рисунке жирными стрелками); соответствующую последовательность можно найти, проследовав по указателям в обратном направлении от наилучшего заключительного состояния.

Рис. 15.4. Пример применения алгоритма Витерби: возможные последовательности состояний для переменной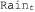могут рассматриваться как пути через граф возможных состояний на каждом временном интервале (состояния обозначены прямоугольниками для предотвращения путаницы с узлами в байесовской сети) (а); результаты применения алгоритма Витерби к последовательности наблюдений за появлением директора с зонтиком, [true, true, false, true, true] (б). Для каждого значения t показано значение сообщения, которое представляет собой вероятность наилучшей последовательности, достигающей каждого состояния во время t. Кроме того, для каждого состояния ведущая в него жирная стрелка показывает его наилучшего преемника, согласно оценке, представляющей собой произведение вероятности предшествующей последовательности и вероятности перехода. Наиболее вероятную последовательность можно определить, проходя по жирным стрелкам в обратном направлении от наиболее вероятного состояния в интервале времени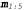

Только что описанный алгоритм называется алгоритмом Витерби в честь его разработчика. Временная сложность этого алгоритма, как и алгоритма фильтрации, линейно зависит от t, от длины последовательности. Но в отличие от алгоритма фильтрации его потребность в пространстве также линейно зависит от t. Это связано с тем, что в алгоритме Витерби необходимо следить за указателями, которые обозначают наилучшую последовательность, ведущую к каждому состоянию.