|
Страница 4 из 5 Таким образом, было показано, что если будет обеспечено правильное сопровождение S- и G-множества в соответствии с их определениями, то эти множества обеспечат удовлетворительное представление пространства версий. Остается единственная проблема — как обновлять S- и G-множество с учетом нового примера (выполнение этой операции возложено на функцию Version-Space-Update). На первый взгляд эта задача может показаться довольно затруднительной, но на основе определений множеств и с помощью рис. 19.2 не слишком сложно составить необходимый для этого алгоритм. Необходимо прежде всего обеспечить использование элементов из S- и G-множества соответственно. Применительно к каждому из таких элементов каждый новый экземпляр примера может быть ложно положительным или ложно отрицательным. Возникающие при этом варианты описаны ниже. из S- и G-множества соответственно. Применительно к каждому из таких элементов каждый новый экземпляр примера может быть ложно положительным или ложно отрицательным. Возникающие при этом варианты описаны ниже. 1. Ложно положительный пример для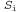 . Появление такого примера означает, что гипотеза . Появление такого примера означает, что гипотеза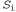 является слишком общей, но (по определению) совместимое уточнение для гипотезы является слишком общей, но (по определению) совместимое уточнение для гипотезы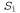 отсутствует, поэтому ее необходимо исключить из S-множества. отсутствует, поэтому ее необходимо исключить из S-множества. 2. Ложно отрицательный пример для . Появление такого примера означает, что гипотеза . Появление такого примера означает, что гипотеза является слишком конкретной, поэтому она заменяется всеми своими непосредственными обобщениями, при соблюдении условия, что они остаются более конкретными, чем любой элемент G-множества. является слишком конкретной, поэтому она заменяется всеми своими непосредственными обобщениями, при соблюдении условия, что они остаются более конкретными, чем любой элемент G-множества. 3. Ложно положительный пример для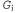 . Появление такого примера означает, что гипотеза . Появление такого примера означает, что гипотеза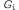 является слишком общей, поэтому она заменяется всеми своими непосредственными уточнениями, при соблюдении условия, что они остаются более общими, чем любой элемент S-множества. является слишком общей, поэтому она заменяется всеми своими непосредственными уточнениями, при соблюдении условия, что они остаются более общими, чем любой элемент S-множества. 4. Ложно отрицательный пример для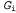 . Появление такого примера означает, что гипотеза . Появление такого примера означает, что гипотеза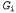 является слишком конкретной, но (по определению) совместимое обобщение для гипотезы является слишком конкретной, но (по определению) совместимое обобщение для гипотезы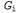 отсутствует, поэтому ее необходимо исключить из G-множества. отсутствует, поэтому ее необходимо исключить из G-множества. Указанные выше операции продолжаются применительно к каждому новому экземпляру примера до тех пора, пока не произойдет одно из перечисленных ниже событий. 1. В пространстве версий останется одно и только одно определение некоторой концепции, и в этом случае оно будет возвращено как уникальная гипотеза. 2. Пространство версий свернется (либо S-, либо G-множество станет пустым), и это будет означать, что для данного обучающего множества не существуют совместимые гипотезы. Такая ситуация аналогична неудачному завершению поиска, которое возникает в простом варианте алгоритма формирования дерева решений. 3. Примеры закончатся, а в пространстве версий останется несколько гипотез. Это означает, что пространство версий представляет собой дизъюнкцию гипотез. Если при поступлении любого нового примера все дизъюнкты этой дизъюнкции согласуются, то можно возвратить определяемую ими классификацию данного примера. Если же они не согласуются, один из вариантов состоит в использовании мажоритарного голосования.
|