Timisoara; поскольку функция " является допустимой, рассматриваемый алгоритм может безопасно игнорировать это поддерево, гарантируя вместе с тем оптимальность. Понятие отсечения (под которым подразумевается исключение из рассмотрения некоторых вариантов в связи с отсутствием необходимости их исследовать) является важным для многих областей искусственного интеллекта.

Одно заключительное наблюдение состоит в том, что среди оптимальных алгоритмов такого типа (алгоритмов, которые развертывают пути поиска от корня) поиск А* является оптимально эффективным для любой конкретной эвристической функции. Это означает, что не гарантируется развертывание меньшего количества узлов, чем в поиске А*, с помощью какого-либо иного оптимального алгоритма (не считая той возможности, когда осуществляется выбор на равных среди узлов с f(n) =C*). Это связано с тем, что любой алгоритм, который не развертывает все узлы со значениями f{n)<C*, подвержен риску потери оптимального решения.

Те соображения, что поиск А*, как один из всех подобных алгоритмов, является действительно полным, оптимальным и оптимально эффективным, оставляют довольно приятное впечатление. Но, к сожалению, это отнюдь не означает, что поиск А* может служить ответом на все наши потребности в поиске. Сложность заключается в том, что при решении большинства задач количество узлов в пределах целевого контура пространства состояний все еще зависит экспоненциально от длины решения. Хотя доказательство этого утверждения выходит за рамки настоящей книги, было показано, что экспоненциальный рост происходит, если ошибка эвристической функции растет не быстрее по сравнению с логарифмом фактической стоимости пути. В математических обозначениях условие субэкспоненциального роста состоит в следующем: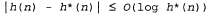