|
Страница 2 из 2 Если даны три точки,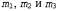 , в модели, не лежащие на одной прямой, и их масштабированные ортогональные проекции, , в модели, не лежащие на одной прямой, и их масштабированные ортогональные проекции,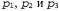 , на плоскости изображения, то существуют две и только две трансформации из системы координат трехмерной модели в систему координат двухмерного изображения. , на плоскости изображения, то существуют две и только две трансформации из системы координат трехмерной модели в систему координат двухмерного изображения. Эти трансформации связаны друг с другом, поскольку зеркально противоположны относительно плоскости изображения; они могут быть вычислены на основе простого решения в замкнутой форме. Если существует возможность идентифицировать характеристики модели, соответствующие трем характеристикам в изображении, то может быть вычислена Q— поза объекта. В предыдущем подразделе обсуждался метод определения соответствий с использованием согласования контекстов формы. Если же объект имеет четко определенные углы или другие заметные точки, то становится доступным еще более простой метод. Идея его состоит в том, что необходимо повторно формировать и проверять соответствия. Мы должны выдвинуть первоначальную гипотезу о соответствии тройки точек изображения тройке точек модели и использовать функцию Find-Transform для формирования гипотезы Q. Если принятое предположение о соответствии было правильным, то трансформация Q является правильной и после ее применения к оставшимся точкам модели приводит к получению предсказания координат точек изображения. Если принятое предположение было неправильным, то трансформация Q также является неправильной и после ее применения к оставшимся точкам модели не позволяет предсказывать координаты точек изображения. Описанный выше подход лежит в основе алгоритма Align, приведенного в листинге 24.1. Этот алгоритм находит позу для данной конкретной модели или возвращает индикатор неудачи. Временная сложность данного алгоритма в худшем случае пропорциональна количеству сочетаний троек точек модели и троек точек изображения, или 
умноженному на стоимость проверки каждого сочетания. Стоимость проверки пропорциональна MlogN, поскольку необходимо предсказывать позицию изображения для каждой из Μ точек модели и находить расстояние до ближайшей точки изображения, что требует выполнения logN операций, если точки изображения представлены с помощью некоторой подходящей структуры данных. Поэтому в наихудшем случае сложность алгоритма выравнивания определяется значением  , где М и N— количество точек модели и изображения соответственно. Методы, основанные на принципе кластеризации поз в сочетании со средствами рандомизации, позволяют уменьшить сложность до , где М и N— количество точек модели и изображения соответственно. Методы, основанные на принципе кластеризации поз в сочетании со средствами рандомизации, позволяют уменьшить сложность до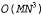 . Результаты применения этого алгоритма к изображению степлера показаны на рис. 24.21. . Результаты применения этого алгоритма к изображению степлера показаны на рис. 24.21. Листинг 24.1. Неформальное описание алгоритма выравнивания 
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|