|
Страница 2 из 3 Уравнение 10.3 называется дополнением уравнения 10.2. Вообще говоря, такое дополнение должно содержать определение для каждого предиката (высказывание в форме "тогда и только тогда"), а каждое определение должно содержать по одному дизъюнкту для каждого определенного выражения, головой которого является этот предикат. Как правило, такое дополнение создается, как описано ниже. 1. Собрать все выражения с одним и тем же названием предиката (Р) и с одной и той же арностью (л). 2. Преобразовать каждое выражение в нормальную форму Кларка, например, заменить выражение 
где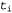 — термины, выражением — термины, выражением 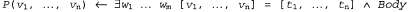
где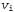 — вновь введенные переменные, а — вновь введенные переменные, а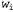 — переменные, которые присутствуют в первоначальном выражении. При этом следует использовать одно и то же множество vi для каждого выражения. Это приводит к получению такого множества выражений: — переменные, которые присутствуют в первоначальном выражении. При этом следует использовать одно и то же множество vi для каждого выражения. Это приводит к получению такого множества выражений: 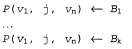
3. Скомбинировать их вместе в одно большое дизъюнктивное выражение: 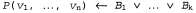
4. Сформировать завершение, заменяя оператор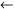 оператором эквивалентности: оператором эквивалентности: 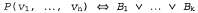
Пример дополнения Кларка для базы знаний, включающей и базовые факты, и правила, приведен в табл. 10.2. Чтобы ввести в действие предположение об уникальности имен, достаточно сформировать дополнение Кларка для отношения равенства, где единственными известными фактами являются CS=CS, 101 = 101 и т.д. Оставляем эту задачу читателю в качестве упражнения. Таблица 10.2. Дополнение Кларка для множества хорновских выражений. В первоначальной хорнов-ской программе (слева) четыре курса перечислены явно, а также содержатся утверждения, что проводятся курсы по математике с целочисленными номерами от 101 до 130, а для каждого курса CS по компьютерным наукам в серии 100 (для студентов) имеется соответствующий курс в серии 200 (для аспирантов). В дополнении Кларка (справа) указано, что других курсов больше нет. С помощью этого дополнения и предположения об уникальности имен (а также очевидного определения предиката Integer) можно получить желаемое заключение, что имеется точно 36 курсов: 30 курсов по математике и 6 курсов по компьютерным наукам 
 Предположение о замкнутом мире позволяет найти минимальную модель отношения. Это означает, что в данном примере можно найти модель отношения Course с наименьшим количеством элементов. Минимальная модель отношения Course, соответствующая уравнению 10.2, имеет четыре элемента; при меньшем количестве элементов возникало бы противоречие. Для хорновских баз знаний всегда имеется уникальная минимальная модель. Следует отметить, что с учетом предположения об уникальности имен это утверждение распространяется также и на отношение равенства, поскольку каждый терм равен только самому себе. Как ни парадоксально, это означает также, что минимальные модели являются одновременно и максимальными, в том смысле, что включают максимально возможное количество объектов.
|