При решении обычных задач поиска оптимальное решение для игрока мах должно представлять собой последовательность ходов, ведущих к цели — к терминальному состоянию, которое соответствует выигрышу. С другой стороны, в игре

участвует также игрок MIN, который имеет другое мнение по этому поводу. Это означает, что игрок МАХ должен найти надежную стратегию, позволяющую определить ход игрока МАХ в начальном состоянии, затем ходы игрока МАХ в состояниях, ставших результатом любого возможного ответа игрока MIN, а затем ходы МАХ в состояниях, ставших результатом любого возможного ответа MIN на те ходы, и т.д. Грубо говоря, оптимальная стратегия приводит к итогу, по меньшей мере, такому же благоприятному, как и любая другая стратегия, в тех условиях, когда приходится играть с противником, не допускающим ошибок. Прежде всего рассмотрим, как найти эту оптимальную стратегию, даже притом что для МАХ часто будет неосуществимой задача ее исчерпывающего вычисления в играх, более сложных, чем крестики-нолики.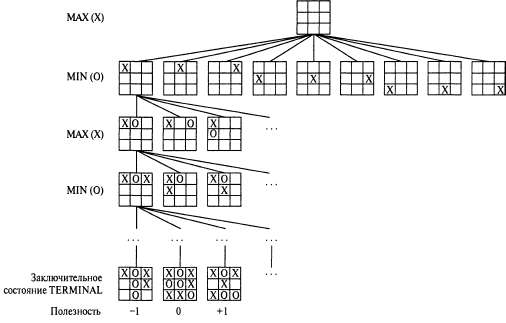

Рис. 6.1. (Частичное) дерево поиска для игры крестики-нолики. Верхний узел представляет собой начальное состояние, а первым ходит игрок МАХ, ставя значок X в пустой клетке. На этом рисунке показана часть дерева поиска, в которой демонстрируются чередующиеся ходы игроков MIN (значок О) и МАХ (значок X). Ходы выполняются до тех пор, пока в конечном итоге не будет достигнуто одно из терминальных состояний, которым могут быть назначены данные о полезности в соответствии с правилами игры