|
Страница 2 из 3 Даже такие простые игры, как крестики-нолики, являются слишком сложными, чтобы можно было привести в этой книге для них полное дерево игры, поэтому перейдем к описанию тривиальной игры, показанной на рис. 6.2. Возможные коды игрока МАХ из корневого узла обозначены как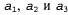 . Возможными ответами на ход а1 для игрока MIN являются . Возможными ответами на ход а1 для игрока MIN являются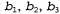 и т.д. Данная конкретная игра заканчивается после того, как каждый игрок, МАХ и MIN, сделают по одному ходу. (Согласно терминологии теории игр, это дерево имеет глубину в один ход и состоит из сделанных двумя участниками ходов, каждый из которых называется полуходом.) Полезности терминальных состояний в этой игре находятся в пределах от 2 до 14. и т.д. Данная конкретная игра заканчивается после того, как каждый игрок, МАХ и MIN, сделают по одному ходу. (Согласно терминологии теории игр, это дерево имеет глубину в один ход и состоит из сделанных двумя участниками ходов, каждый из которых называется полуходом.) Полезности терминальных состояний в этой игре находятся в пределах от 2 до 14. 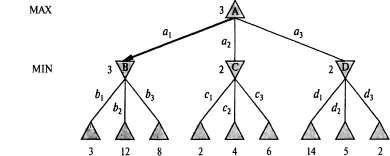 Рис. 6.2. Дерево игры с двумя полуходами. Узлы А представляют собой "узлы МАХ", в которых очередь хода принадлежит игроку МАХ, а узлы рассматриваются как "узлы MIN". Терминальные узлы показывают значения полезности для МАХ; остальные узлы обозначены их минимаксными значениями. Лучшим ходом игрока МАХ от корня является а.1, поскольку ведет к преемнику с наибольшим минимаксным значением, а наилучшим ответом MIN является b1i, поскольку ведет к преемнику с наименьшим минимаксным значением При наличии дерева игры оптимальную стратегию можно определить, исследуя минимаксное значение каждого узла, которое можно записать как Minimax-Value (n). Минимаксным значением узла является полезность (для МАХ) пребывания в соответствующем состоянии, при условии, что оба игрока делают ходы оптимальным образом от этого узла и до узла, обозначающего конец игры. Очевидно, что минимаксным значением терминального состояния является просто его полезность. Более того, если есть выбор, игрок МАХ должен предпочесть ход, ведущий в состояние с максимальным значением, а игрок MIN — ведущий в состояние с минимальным значением. Поэтому имеет место приведенное ниже соотношение.
|