Многие популярные игры допускают наличие больше чем двух игроков. Рассмотрим, как можно распространить идею минимаксного алгоритма на игры с несколькими игроками. С точки зрения технической реализации это сделать несложно, но при этом возникают некоторые новые и интересные концептуальные проблемы.

Вначале необходимо заменить единственное значение для каждого узла вектором значений. Например, в игре с тремя игроками, в которой участвуют игроки А, В и С, с каждым узлом ассоциируется вектор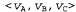. Для терминальных состояний этот вектор задает полезность данного состояния с точки зрения каждого игрока. (В играх с двумя игроками и нулевой суммой двухэлементный вектор может быть сокращен до единственного значения, поскольку значения в нем всегда противоположны.) Простейшим способом реализации такого подхода является применение функции Utility, которая возвращает вектор значений полезности.

Теперь необходимо рассмотреть нетерминальные состояния. Рассмотрим узел в дереве игры, показанном на рис. 6.3, который обозначен как X. В этом состоянии игрок С выбирает, что делать. Два варианта ведут к терминальным состояниям с векторами полезности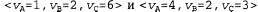. Поскольку 6 больше чем 3, игрок С должен выбрать первый ход. Это означает, что если достигнуто состояние X, то дальнейшая игра приведет к терминальному состоянию с полезностя-ми. Следовательно, зарезервированным значением X является этот вектор. Вообще говоря, зарезервированное значение узла п представляет собой вектор полезности такого узла-преемника, который имеет наивысшее значение для игрока, выбирающего ход в узле п.