|
Страница 3 из 4 По причинам, которые вскоре станут очевидными, до конца этой главы предполагается, что используются обесцениваемые вознаграждения, хотя иногда допускается применение значения γ=1. Сделанный нами выбор бесконечных горизонтов становится причиной возникновения определенной проблемы: если среда не содержит терминальное состояние или если агент никогда его не достигает, то все истории пребывания в среде будут иметь бесконечную длину, а полезности, связанные с аддитивными вознаграждениями, в общем случае будут бесконечными. Дело в том, что, безусловно, лучше, чем лучше, чем , но гораздо сложнее сравнивать две последовательности состояний, притом что обе имеют полезность , но гораздо сложнее сравнивать две последовательности состояний, притом что обе имеют полезность . Для решения этой проблемы можно применить три описанных ниже подхода, два из которых уже упоминались в этой главе. . Для решения этой проблемы можно применить три описанных ниже подхода, два из которых уже упоминались в этой главе. 1. При наличии обесцениваемых вознаграждений полезность любой бесконечной последовательности является конечной. В действительности, если вознаграждения ограничены значением и γ<1, то можно получить следующее соотношение с использованием стандартной формулы суммы бесконечных геометрических рядов: и γ<1, то можно получить следующее соотношение с использованием стандартной формулы суммы бесконечных геометрических рядов: 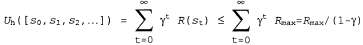 (17.1) (17.1)
2. Если среда содержит терминальные состояния и гарантируется достижение агентом в конечном итоге одного из этих состояний, то нам никогда не придется сравнивать бесконечные последовательности действий. Стратегия, который гарантирует достижение терминального состояния, называется правильной стратегией. При наличии правильных стратегий можно использовать γ=1 (т.е. аддитивные вознаграждения). Первые три стратегии, показанные на рис. 17.2, б, являются правильными, а четвертая — неправильной. В ней достигается бесконечное суммарное вознаграждение за счет предотвращения попадания в терминальные состояния, притом что вознаграждение за пребывание в нетерминальных состояниях является положительным. Само существование неправильных стратегий в сочетании с использованием аддитивных вознаграждений может стать причиной неудачного завершения стандартных алгоритмов решения задач MDP, поэтому является весомым доводом в пользу применения обесцениваемых вознаграждений. 3. Еще один подход состоит в том, чтобы сравнивать бесконечные последовательности по среднему вознаграждению, получаемому в расчете на каждый временной интервал. Предположим, что с квадратом (1,1) в мире 4x3 связано вознаграждение 0.1, тогда как для других нетерминальных состояний предусмотрено вознаграждение 0.01. В таком случае стратегия, в которой агент предпочтет оставаться в квадрате (1,1), позволит получать более высокое среднее вознаграждение по сравнению с той стратегией, в которой агент находится в каком-то другом квадрате. Среднее вознаграждение представляет собой полезный критерий для некоторых задач, но анализ алгоритмов со средним вознаграждением выходит за рамки данной книги.
|