|
Страница 1 из 2 До сих пор предполагалось, что структура байесовской сети задана, и мы просто пытаемся определить в процессе обучения ее параметры, тогда как структура самой сети представляет основные причинные знания о проблемной области, которые часто может без особых затруднений сформулировать не только специалист, но даже неопытный пользователь. Но в некоторых случаях причинная модель может оказаться недоступной или стать предметом спора (например, некоторые корпорации долгое время утверждали, что курение не является причиной рака), поэтому важно понять, как может быть определена путем обучения структура байесовской сети на основе данных. В настоящее время алгоритмы структурного обучения находятся на начальном этапе развития, поэтому в данном разделе будет приведен лишь краткий обзор основных идей. Наиболее очевидным подходом к решению этой задачи является поиск качественной модели. Эту работу можно начать с модели, не содержащей связей, и приступить к введению родительских узлов для каждого узла, согласуя параметры с помощью только что описанных методов и измеряя точность результирующей модели. Еще один вариант состоит в том, что можно начать с исходного предположения о структуре и использовать поиск с восхождением к вершине или с эмуляцией отжига для внесения модификаций, возвращая параметры после каждого изменения в структуре. Модификации могут включать обращение, добавление или удаление дуг. В этом процессе следует избегать появления циклов, поскольку во многих алгоритмах принято предположение, что для переменных задано упорядочение и что узел может иметь родительские узлы только среди тех узлов, которые присутствуют перед ним в этом упорядочении (точно так же, как и в процессе создания сети, описанном в главе 14). Для достижения полной общности необходимо также обеспечить поиск среди возможных упорядочений. Существуют два альтернативных метода принятия решения о том, нужно ли прекратить поиск, поскольку обнаружена приемлемая структура. Первый из них предусматривает проверку того, действительно ли в данных удовлетворяются предположения об условной независимости, неявно заданные в этой структуре. Например, сам факт использования наивной байесовской модели для задачи с рестораном равносилен предположению о том, что справедливо приведенное ниже соотношение, поэтому можно проверить по самим данным, соблюдается ли это соотношение применительно к соответствующим условным частотам. 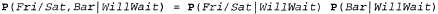
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|