|
Страница 1 из 2 Ответы на эти вопросы можно получить, записав некоторые ограничения, распространяющиеся на предпочтения, которые должен иметь рациональный агент, а затем показав, что принцип MEU можно вывести из этих ограничений. Для описания предпочтений агента будут использоваться приведенные ниже обозначения. 
Теперь напрашивается очевидный вопрос, к какого рода понятиям относятся А и в? Если действия агента являются детерминированными, то А и в обычно представляют собой конкретные, полностью заданные результирующие состояния этих действий. В более общем, недетерминированном случае А и В представляют собой лотереи. Лотерея по сути является распределением вероятностей по множеству фактических результатов ("призов" в лотерее). Лотерея L с возможными результатами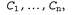 которые могут возникать с вероятностями которые могут возникать с вероятностями записывается следующим образом: записывается следующим образом: 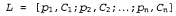
(Лотерея только с одним результатом может быть записана либо как А, либо как [1,А].) Вообще говоря, каждым результатом лотереи может быть атомарное состояние или другая лотерея. Основная проблема теории полезности состоит в том, чтобы понять, как предпочтения между сложными лотереями связаны с предпочтениями между основополагающими состояниями в этих лотереях. Для этого мы должны наложить на это отношение предпочтения приемлемые ограничения, во многом аналогично тому, как были наложены ограничения рациональности на степени уверенности для получения аксиом вероятностей в главе 13. Одно из разумных ограничений состоит в том, что предпочтение должно быть транзитивным, т.е. если то следует ожидать, что то следует ожидать, что Свойство транзитивности можно обосновать, показав, что агент, предпочтения которого не соответствуют свойству транзитивности, будет вести себя нерационально. Предположим, например, что агент имеет нетранзитивное предпочтение Свойство транзитивности можно обосновать, показав, что агент, предпочтения которого не соответствуют свойству транзитивности, будет вести себя нерационально. Предположим, например, что агент имеет нетранзитивное предпочтение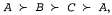 где А, в и С— товары, которые могут свободно обмениваться друг на друга. Если агент в настоящее время имеет товар А, то можно предложить обменять С на А и немного наличных. где А, в и С— товары, которые могут свободно обмениваться друг на друга. Если агент в настоящее время имеет товар А, то можно предложить обменять С на А и немного наличных.
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|