|
Страница 4 из 4 До сих пор персептроны рассматривались как средства реализации детерминированных функций, выходные данные которых могут содержать ошибки. Выход сиг-моидального персептрона можно также интерпретировать как вероятность, а именно вероятность того, что истинным выходом является 1, если заданы все входы. При такой интерпретации сигмоидальный персептрон может использоваться как каноническое представление для условных распределений в байесовских сетях (см. раздел 14.3). Существует также возможность выполнять вероятностный вывод правила обучения с использованием стандартного метода максимизации (условного) логарифмического правдоподобия данных, как было описано выше в данной главе. Рассмотрим, как действует последний метод. Допустим, что рассматривается единственный обучающий пример с истинным выходным значением Т, и предположим, что р— вероятность, возвращаемая пер-септроном для этого примера. Если T=1, то условная вероятность этих данных равна ρ, а если T=0, то условная вероятность данных равна (1-р). Теперь можно воспользоваться простым приемом, чтобы записать интересующее нас выражение для логарифмического правдоподобия в дифференцируемой форме. Этот прием состоит втом, что переменная со значениями 0/1 в экспоненте выражения рассматривается как индикаторная переменная: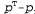 , если т=1, и 1 — в противном случае; аналогичным образом, , если т=1, и 1 — в противном случае; аналогичным образом,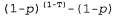 , если т=0, и 1 — в противном случае. Поэтому можно записать выражение для логарифмического правдоподобия данных следующим образом: , если т=0, и 1 — в противном случае. Поэтому можно записать выражение для логарифмического правдоподобия данных следующим образом:  (20.13) (20.13)
В силу самих свойств сигмоидальной функции полученный градиент сводится к очень простой формуле (упр. 20.16): 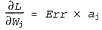
Обратите внимание на то, что вектор обновления весов для обучения с максимальным правдоподобием в сигмоидальных персептронах по сути идентичен вектору обновления для минимизации квадратичной ошибки. Таким образом, можно утверждать, что персептроны имеют вероятностную интерпретацию, даже если правило их обучения выведено на основании детерминированного подхода.
<< В начало < Предыдущая 1 2 3 4 Следующая > В конец >>
|