Итак, W · χ = 0 определяет гиперплоскость в пространстве входных данных, поэтому персептрон возвращает 1 тогда и только тогда, когда входные данные находятся с одной стороны от этой гиперплоскости. По такой причине пороговый персептрон называют линейным разделителем. На рис. 20.20, а, б показана такая гиперплоскость (которая в двух измерениях является линией) для представления с помощью персептрона функций AND и OR от двух входных значений. Черные кружки обозначают точки в пространстве входных данных, где значение этой функции равно 1, а белые кружки — точки, где это значение равно 0. Персептрон способен представить эти функции, поскольку есть какая-то линия, которая отделяет все белые кружки от всех черных кружков. Такие функции называются линейно разделимыми. На рис. 20.20, в показан пример функции, которая не является линейно разделимой, — функции XOR. Безусловно, что пороговый персептрон не позволяет определить в процессе обучения эту функцию. Вообще говоря, пороговые персептроны способны представить только линейно разделимые функции. Но такие функции составляют лишь небольшую часть всех функций; в упр. 20.14 предлагается определить величину этой части. Сигмоидальные персептроны характеризуются аналогичными ограничениями, с той поправкой, что они представляют только "мягкие" линейные разделители (см. рис. 20.19, б).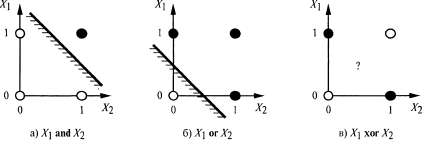

Рис. 20.20. Иллюстрация свойства линейной разделимости пороговых персептро-нов. Черные кружки показывают тонки в пространстве входных данных, где значение функции равно 1, а белые кружки показывают точки, где это значение равно 0. Персептрон возвращает 1 при получении данных из области, соответствующей незаштрихованной стороне линии. На рис. 20.20, в не существует такой линии, которая могла бы правильно классифицировать входные данные

Несмотря на их ограниченную выразительную мощь, пороговые персептроны имеют некоторые преимущества. В частности, существует простой алгоритм обучения, позволяющий выполнить подгонку весов порогового персептрона к любому линейно разделимому обучающему множеству, но в данном разделе вместо описания этого алгоритма мы выведем тесно связанный с ним алгоритм для обучения с помощью сигмоидальных персептронов.

В основе этого алгоритма, а в действительности в основе большинства алгоритмов для обучения нейронных сетей, лежит такая идея, что в процессе обучения необходимо корректировать веса в сети для минимизации некоторого критерия измерения ошибок в обучающем множестве. Таким образом, задача обучения формулируется как некоторая задача оптимизационного поиска в пространстве весов. "Классическим" критерием измерения ошибок является сумма квадратичных ошибок, которая использовалась в том числе в алгоритме линейной регрессии, приведенном на с. 1. Квадратичная ошибка для единственного обучающего примера с входными данными x и истинными выходными данными у определяется следующим образом:

где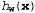— выходные данные персептрона при обработке рассматриваемого примера.