Последнее приложение алгоритма ЕМ, рассматриваемой в данной главе, касается изучения вероятностей перехода в скрытых марковских моделях (Hidden Markov Model— HMM). Напомним, что, как было сказано в главе 15, скрытая марковская модель может быть представлена с помощью динамической байесовской сети с одной дискретной переменной состояния (рис. 20.11). Каждая точка данных состоит из последовательности наблюдений конечной длины, поэтому задача заключается в том, чтобы определить в процессе обучения вероятности перехода на основании множества последовательностей наблюдений (или, возможно, на основании только одной длинной последовательности).

Рис. 20.11. Развернутая динамическая байесовская сеть, которая представляет скрытую марковскую модель (повторение рис. 15.12)

В данной главе уже было показано, как проводить обучение байесовских сетей, но в этом случае возникает одна сложность: в байесовских сетях каждый параметр является различным, а в скрытой марковской модели, с другой стороны, отдельные вероятности перехода из состояния i в состояния j во время t, , повторяются во времени, т.е.для всех t. Чтобы оценить вероятность перехода из состояния i в состояние j, достаточно вычислить ожидаемую долю случаев, в которых система подвергается переходу в состояние j, находясь в состоянии i: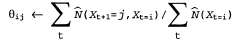

Опять-таки эти ожидаемые количества могут быть вычислены с помощью любого алгоритма вероятностного вывода для скрытой марковской модели. Для вычисления необходимых вероятностей можно очень легко модифицировать прямой—обратный алгоритм, приведенный в листинге 15.1. Заслуживает внимание одно важное замечание, что требуются вероятности, полученные путем сглаживания, а не фильтрации; это означает, что при оценке вероятности того, что произошел конкретный переход, необходимо учитывать полученное впоследствии свидетельство. Например, как было указано в главе 15, свидетельство в случае убийства обычно может быть получено только после этого преступления (т.е. после перехода из состояния i в состояние j).