Обучение параметрам с помощью метода максимального правдоподобия: дискретные модели

Допустим, что мы покупаем пакет конфет с лимонными и вишневыми леденцами, выпущенный новым изготовителем, соотношение лимонных и вишневых леденцов в продукции которого полностью неизвестно; это означает, что доля тех и других леденцов может измеряться любым значением от 0 до 1. В данном случае приходится рассматривать континуум гипотез. Кроме того, в этом случае параметром, который будет обозначаться как Θ, является доля вишневых леденцов, а гипотезой является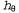(доля лимонных леденцов выражается как 1-Θ). Если принято предположение, что все возможные значения долевого состава априорно являются равновероятными, то становится обоснованным подход на основе гипотезы с максимальным правдоподобием. Если мы промоделируем эту ситуацию с помощью байесовской сети, то потребуется только одна случайная переменная, Flavor (разновидность конфеты, случайно выбранной из пакета). Эта переменная принимает значения cherry и lime, где вероятность cherry равна θ (рис. 20.2, а). Теперь предположим, что развернуто N конфет, из которых с оказались вишневыми леденцами, а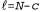были лимонными леденцами. Согласно уравнению 20.3, правдоподобие этого конкретного набора данных выражается следующей формулой:

Гипотеза с максимальным правдоподобием задается значением Θ, которое максимизирует это выражение. Такое же значение может быть получено путем максимизации значения логарифмического правдоподобия:

(Взяв логарифмы, мы преобразовали произведение в сумму по данным, которую обычно легче максимизировать.) Чтобы найти значение максимального правдоподобия Θ, дифференцируем L по θ и приравняем полученное выражение к нулю следующим образом: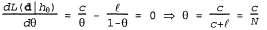

Таким образом, если описать это выражение на естественном языке, то гипотеза с максимальным правдоподобиемутверждает, что фактическая доля вишневых леденцов в пакете равна наблюдаемой доле этих леденцов в конфетах, развернутых до сих пор!

На первый взгляд создается впечатление, что мы проделали большой объем работы лишь для того, чтобы открыть этот очевидный факт. Но в действительности описанным выше путем был создан один из стандартных методов обучения параметрам с максимальным правдоподобием, который описан ниже.

1.    Записать выражение для правдоподобия данных как функции от параметра (параметров).

2.    Найти производную логарифмического правдоподобия по отношению к каждому параметру.

3.    Найти такие значения параметров, чтобы производные стали равными нулю.