Обычно самым сложным является последний из этих этапов. В рассматриваемом примере он был простейшим, но ниже будет показано, что во многих случаях приходится прибегать к использованию итерационных алгоритмов поиска решений или других числовых методов оптимизации, как было описано в главе 4. Кроме того, этот пример иллюстрирует важную проблему, которая в целом характерна для обучения с учетом максимального правдоподобия: если набор данных достаточно мал и поэтому некоторые события еще не наблюдались (например, не было обнаружено ни одной конфеты с вишневым леденцом), то гипотеза с максимальным правдоподобием одной конфеты с вишневым леденцом), то гипотеза с максимальным правдоподобием присваивает этим событиям нулевую вероятность. Для предотвращения возникновения этой проблемы использовались различные приемы, такие как инициализация счетчиков для каждого события значением 1, а не 0.

Рассмотрим еще один пример. Предположим, что этот новый изготовитель конфет хочет дать потребителю небольшую подсказку и использует для конфет обертки красного и зеленого цветов. Значение переменной Wrapper, соответствующей цвету обертки для каждой конфеты, выбирается по вероятностным законам, в соответствии с некоторым неизвестным условным распределением, но в зависимости от разновидностей конфет. Соответствующая вероятностная модель показана на рис. 20.2, б. Обратите внимание на то, что она имеет три параметра: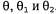. С использованием этих параметров правдоподобие события, связанного, скажем, с обнаружением вишневого леденца в зеленой обертке, можно определить на основе стандартной семантики для байесовских сетей: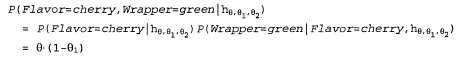

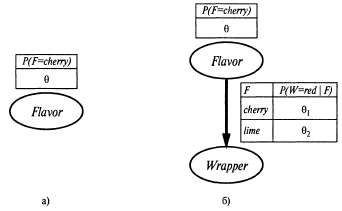
Рис. 20.2. Обучение параметром с помощью байесовской сети: модель в виде байесовской сети для случая, в котором доля вишневых и лимонных леденцов в пакете неизвестна (а); модель для того случая, когда цвета обертки связаны (вероятностной) зависимостью с разновидностями конфет (б)