|
Страница 2 из 2 Теперь рассмотрим линейную гауссову модель с одним непрерывным родительским значением X и непрерывным дочерним значением Υ. Как было описано , значение Υ имеет гауссово распределение, математическое ожидание которого линейно зависит от значения X, а среднеквадратичное отклонение является постоянным. Чтобы определить в результате обучения распределение условных вероятностей Р( Υ\ Χ), можно максимизировать условное правдоподобие следующим образом: 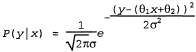 (20.5) (20.5)
где параметрами являются θ1, θ2 и σ. Данные представляют собой множество пар 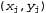 , как показано на рис. 20.4. Используя обычные методы, можно найти значения параметров с максимальным правдоподобием. Но в этом контексте нужно сделать еще одно замечание. Если рассматриваются только параметры θ1 и θ2, которые определяют линейную связь между χ и у, то становится очевидно, что максимизация логарифмического правдоподобия по отношению к этим параметрам равносильна минимизации числителя в экспоненте уравнения 20.5: , как показано на рис. 20.4. Используя обычные методы, можно найти значения параметров с максимальным правдоподобием. Но в этом контексте нужно сделать еще одно замечание. Если рассматриваются только параметры θ1 и θ2, которые определяют линейную связь между χ и у, то становится очевидно, что максимизация логарифмического правдоподобия по отношению к этим параметрам равносильна минимизации числителя в экспоненте уравнения 20.5: Рис. 20.4. Примеры применения линейной гауссовой модели: линейная гауссова модель, описанная как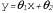 , к которой добавляется гауссов шум с постоянной дисперсией (а); множество из 50 точек данных, сформированных с помощью этой модели (б) , к которой добавляется гауссов шум с постоянной дисперсией (а); множество из 50 точек данных, сформированных с помощью этой модели (б) Величина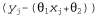 представляет собой ошибку для представляет собой ошибку для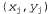 , т.е. разность между фактическим значением , т.е. разность между фактическим значением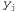 и прогнозируемым значением и прогнозируемым значением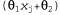 , поэтому ε представляет собой хорошо известную сумму квадратичных ошибок. Она является величиной, которую можно минимизировать с помощью стандартной процедуры линейной регрессии. Теперь можно понять, с чем это связано: минимизация суммы квадратичных ошибок позволяет получить линейную модель с максимальным правдоподобием, при условии, что данные вырабатывались с гауссовым шумом, имеющим постоянную дисперсию. , поэтому ε представляет собой хорошо известную сумму квадратичных ошибок. Она является величиной, которую можно минимизировать с помощью стандартной процедуры линейной регрессии. Теперь можно понять, с чем это связано: минимизация суммы квадратичных ошибок позволяет получить линейную модель с максимальным правдоподобием, при условии, что данные вырабатывались с гауссовым шумом, имеющим постоянную дисперсию.
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|