Как было описано во введении в данной главе, обучение на основе объяснения представляет собой метод извлечения общих правил из отдельных результатов наблюдений. В качестве примера рассмотрим задачу дифференцирования и упрощения алгебраических выражений (упр. 9.15). После выполнения дифференцирования по X такого выражения, как, будет получено выражение 2Х (Обратите внимание на то, что мы используем прописную букву для обозначения арифметического неизвестного X, чтобы отличить его от логической переменной х.) В системе формирования логических рассуждений такая цель может быть выражена как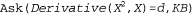 с предполагаемым решением d=2X.

Любой, кто знает дифференциальное исчисление, может найти данное решение, лишь "ознакомившись с условиями задачи", благодаря приобретенным ранее навыкам решения подобных задач. А перед студентом, столкнувшимся с подобными задачами впервые, или перед программой, не накопившей опыта в решении этих задач, возникают гораздо более существенные затруднения. Применение стандартных правил дифференцирования в конечном итоге приводит к получению выражения 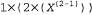, а это выражение в дальнейшем упрощается до 2Х. В логической программной реализации, подготовленной авторами данной книги, для решения такой задачи потребовалось 136 шагов доказательства, причем 99 из этих шагов относились к тупиковым ветвям доказательства. Тот, кто накопил такой отрицательный опыт, вполне естественно, стремится к тому, чтобы та же программа решала аналогичную задачу намного более быстро, встретившись с ней в следующий раз.