|
Страница 1 из 3 Чтобы определить в процессе обучения параметры байесовской сети со скрытыми переменными, можно применить такие же подходы, которые позволили добиться успеха в случае смешанных гауссовых распределений. На рис. 20.10 показана ситуация, в которой имеются два пакета конфет, смешанных друг с другом. Для описания конфет применяются три характеристики: кроме разновидности Flavor и обертки Wrapper, в некоторых конфетах находятся леденцы с отверстиями Hole в середине, а в некоторых — леденцы без отверстий. Распределение конфет в каждом пакете описано с помощью наивной байесовской модели: в каждом конкретном пакете характеристики являются независимыми, но распределение условных вероятностей каждой характеристики зависит от пакета. Применяются следующие параметры: θ — априорная вероятность того, что конфета взята из пакета — вероятности того, что конфета относится к разновидности вишневых леденцов, при условии, что эта конфета взята из пакета Bag 1 и Bag 2 соответственно; — вероятности того, что конфета относится к разновидности вишневых леденцов, при условии, что эта конфета взята из пакета Bag 1 и Bag 2 соответственно;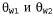 задают вероятности того, что обертка имеет красный цвет; а задают вероятности того, что обертка имеет красный цвет; а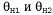 — вероятности того, что леденец имеет отверстие. Обратите внимание на то, что вся эта модель в целом представляет собой модель смешанного распределения (в действительности это смешанное гауссово распределение можно также промоделировать в виде байесовской сети, как показано на рис. 20.10, б). На этом рисунке скрытая переменная соответствует пакету, поскольку после смешивания конфет мы больше не имеем возможности определить, из какого пакета взята каждая конфета. Можно ли в таком случае восстановить описание этих двух пакетов, наблюдая за характеристиками конфет, взятых из этой смеси? — вероятности того, что леденец имеет отверстие. Обратите внимание на то, что вся эта модель в целом представляет собой модель смешанного распределения (в действительности это смешанное гауссово распределение можно также промоделировать в виде байесовской сети, как показано на рис. 20.10, б). На этом рисунке скрытая переменная соответствует пакету, поскольку после смешивания конфет мы больше не имеем возможности определить, из какого пакета взята каждая конфета. Можно ли в таком случае восстановить описание этих двух пакетов, наблюдая за характеристиками конфет, взятых из этой смеси? Проведем одну итерацию алгоритма ЕМ для решения этой задачи. Вначале рассмотрим данные. Сформировано 1000 выборок из модели, истинными параметрами которой являются следующие: 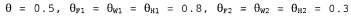 (20.7) (20.7)
Это означает, что равновероятно получение конфет из одного или другого пакета; в первом пакете в основном находятся вишневые леденцы в красных обертках и с отверстиями, а во втором — в основном лимонные леденцы в зеленых обертках и без отверстий. Количество восьми возможных разновидностей конфет определено в табл. 20.1. Рис. 20.10. Примеры применения модели смешанного гауссова распределения и байесовской сети: модель смешанного распределения для задачи с конфетами. Относительные количества различных разновидностей оберток и количества отверстий в леденцах зависят от пакета, который определен с помощью ненаблюдаемой переменной (а); байесовская сеть, соответствующая смешанному гауссову распределению. Среднее и ковариация наблюдаемой переменной X зависит от компонента С (б)
<< В начало < Предыдущая 1 2 3 Следующая > В конец >>
|