Таблица 20.1. Восемь возможных разновидностей конфет

Начнем с инициализации параметров. Для упрощения числовых расчетов выберем следующие значения параметров7:

(20.8)

Вначале проведем расчет для параметра Θ. В полностью наблюдаемом случае можно было бы получить оценку для этого параметра непосредственно из наблюдаемых значений количества конфет, относящихся к пакетам 1 и 2. Но поскольку номер пакета — это скрытая переменная, рассчитаем вместо этого ожидаемые значения количества. Ожидаемое количество N(Bag=l) представляет собой сумму вероятностей того, что конфета взята из пакета 1, по всем конфетам:

Эти вероятности можно вычислить с помощью любого алгоритма вероятностного вывода для байесовских сетей. А применительно к наивной байесовской модели, подобной той, что рассматривается в данном примере, этот вероятностный вывод можно выполнить "вручную", используя правило Байеса и применяя выражение для условной независимости:

(Обратите внимание на то, что нормализующая константа также зависит от параметров.) Применяя эту формулу, например, к данным о 273 конфетах в красной обертке, среди которых находятся вишневые леденцы с отверстиями, определим, какой вклад они вносят в распределение вероятностей:

Продолжая эти расчеты для семи других видов конфет, количество которых указано в табл. 20.1, получим, что = 0.6124.

Теперь рассмотрим другие параметры, такие как. В полностью наблюдаемом случае это значение можно было бы оценить непосредственно на основе наблюдаемых значений количества вишневых и лимонных леденцов из пакета 1. Ожидаемое количество вишневых леденцов из пакета 1 задается с помощью следующего выражения: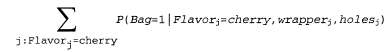

Эти вероятности также можно вычислить с помощью любого алгоритма для байесовской сети. Продолжая этот процесс, получим новые значения для всех параметров:

(20.9)