Наиболее широко используемый метод формирования ансамбля называется усилением. Для того чтобы понять, как он работает, необходимо вначале ознакомиться с идеей взвешенного обучающего множества. В таком обучающем множестве с каждым примером связан вес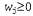. Чем больше вес примера, тем выше важность, присвоенная ему в процессе изучения какой-то гипотезы. Рассматриваемые до сих пор в этой главе алгоритмы обучения несложно модифицировать для работы со взвешенными обучающими множествами5.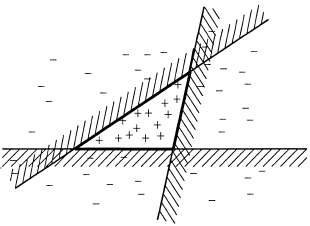

Рис. 18.6. Схема, показывающая, что обучение ансамбля позволяет добиться повышения выразительной мощи гипотез. Здесь представлены три линейные пороговые гипотезы, каждая из которых формирует положительную классификацию на незаштрихованной стороне, а в целом как положительные классифицируются все примеры, которые являются положительными согласно всем трем гипотезам. Полученная в итоге треугольная область представляет собой гипотезу, которая не может быть выражена в первоначальном пространстве гипотез

Процедура усиления начинается с задания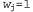для всех примеров (т.е. с обычного обучающего множества). На основании этого множества вырабатывается первая гипотеза, которая классифицирует одни обучающие примеры правильно, а другие — неправильно. Желательно, чтобы следующая гипотеза лучше справлялась с неправильно классифицированными примерами, поэтому веса последних увеличиваются, а веса правильно классифицированных примеров уменьшаются. По этому обучающему множеству со вновь назначенными весами вырабатывается гипотеза h2. Описанный процесс продолжается таким же образом до тех пор, пока не будет выработано Μ гипотез, где м становится входом для алгоритма усиления. Окончательная гипотеза-ансамбль представляет собой взвешенную мажоритарную комбинацию из всех м гипотез, каждой из которых назначен вес, соответствующий тому, насколько высокую производительность она показала при обработке обучающего множества. На рис. 18.7 показана концептуальная иллюстрация работы алгоритма. Эта основная идея усиления имеет много вариантов, в которых применяются различные способы корректировки весов и комбинирования гипотез. В листинге 18.2 показан один из конкретных алгоритмов, называемый AdaBoost. Хотя подробные сведения о том, как происходит корректировка весов, не имеет столь важного значения, алгоритм AdaBoost обладает очень важным свойством: если входной обучающий алгоритм L является слабым обучающим алгоритмом (а это означает, что L всегда возвращает гипотезу со взвешенной ошибкой на обучающем множестве, которая лишь ненамного лучше по сравнению со случайным угадыванием, например, равным 50% при булевой классификации), то алгоритм AdaBoost при достаточно большом значении Μ возвращает гипотезу, идеально классифицирующую обучающие данные. Таким образом, этот алгоритм значительно повышает точность первоначального обучающего алгоритма применительно к обучающим данным. Такой результат остается в силе независимо от того, насколько невыразительным является первоначальное пространство гипотез, а также от того, насколько сложна изучаемая функция.