|
Страница 1 из 2 Приведенные выше результаты анализа иллюстрируют ключевое свойство гауссовых распределений, которое обеспечивает функционирование методов калманов-ской фильтрации: тот факт, что экспонента находится в квадратичной форме. Указанное свойство относится не только к одномерному случаю; полное многомерное гауссово распределение имеет следующую форму: 
Кроме того, произведение термов в экспоненте ясно показывает, что экспонента также является квадратичной функцией от случайных переменных хi которые относятся к х. Как и в одномерном случае, операция обновления фильтрации сохраняет гауссов характер распределения вероятностей состояний. Вначале определим общую временную модель, применяемую в процедуре калма-новской фильтрации. И модель перехода, и модель восприятия позволяют применять линейное преобразование с дополнительным гауссовым шумом. Таким образом, получаем следующее:  (15.19) (15.19)
где F и — матрицы, описывающие линейную модель перехода и ковариацию шума перехода; ни — матрицы, описывающие линейную модель перехода и ковариацию шума перехода; ни — соответствующие матрицы для модели восприятия. Теперь уравнения обновления для среднего и ковариации в их полном, ужасающе сложном виде становятся таковыми: — соответствующие матрицы для модели восприятия. Теперь уравнения обновления для среднего и ковариации в их полном, ужасающе сложном виде становятся таковыми:  (15.20) (15.20)
где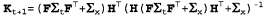 называется калмановской матрицей усиления. Хотите — верьте, хотите — нет, но эти уравнения имеют определенный интуитивный смысл. Например, рассмотрим обновление для оценки значения среднего μ для некоторого состояния. Терм называется калмановской матрицей усиления. Хотите — верьте, хотите — нет, но эти уравнения имеют определенный интуитивный смысл. Например, рассмотрим обновление для оценки значения среднего μ для некоторого состояния. Терм представляет собой прогнозируемое состояние в момент времени t+Ι, поэтому представляет собой прогнозируемое состояние в момент времени t+Ι, поэтому является прогнозируемым результатом наблюдения. Таким образом, терм является прогнозируемым результатом наблюдения. Таким образом, терм соответствует ошибке в прогнозируемых результатах наблюдений. Это значение умножается на соответствует ошибке в прогнозируемых результатах наблюдений. Это значение умножается на  для корректировки прогнозируемого состояния, поэтому для корректировки прогнозируемого состояния, поэтому представляет собой меру того, насколько важными следует считать новые результаты наблюдения применительно к предсказанию. Как и при использовании уравнения 15.18, соблюдается такое свойство, что обновление дисперсии не зависит от результатов наблюдений. Поэтому последовательность значений представляет собой меру того, насколько важными следует считать новые результаты наблюдения применительно к предсказанию. Как и при использовании уравнения 15.18, соблюдается такое свойство, что обновление дисперсии не зависит от результатов наблюдений. Поэтому последовательность значений может быть вычислена в автономном режиме, т.е. фактический объем вычислений, требуемых во время оперативного слежения, становится весьма скромным. может быть вычислена в автономном режиме, т.е. фактический объем вычислений, требуемых во время оперативного слежения, становится весьма скромным.
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|