|
Страница 2 из 2 Для иллюстрации этих уравнений в действии мы применили их к задаче слежения за объектом, движущимся на плоскости χ-γ. Переменными состояния являются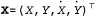 , поэтому , поэтому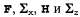 представляют собой матрицы с размерами 4x4. На рис. 15.7, а показаны истинная траектория, ряд зашумленных результатов наблюдения и траектория, оцениваемая с помощью калмановской фильтрации, наряду с ковариациями, указанными с помощью контуров единичного среднеквадратичного отклонения. Процесс фильтрации позволяет весьма успешно следить за фактическим перемещением, к тому же, как и предполагалось, дисперсия быстро достигает фиксированной точки. представляют собой матрицы с размерами 4x4. На рис. 15.7, а показаны истинная траектория, ряд зашумленных результатов наблюдения и траектория, оцениваемая с помощью калмановской фильтрации, наряду с ковариациями, указанными с помощью контуров единичного среднеквадратичного отклонения. Процесс фильтрации позволяет весьма успешно следить за фактическим перемещением, к тому же, как и предполагалось, дисперсия быстро достигает фиксированной точки.  Рис. 15.7. Примеры применения уравнений фильтрации и сглаживания: результаты калмановской фильтрации для объекта, движущегося по плоскости X—Y, которые показывают истинную траекторию (слева направо), ряд зашумленных наблюдений и траекторию, оцениваемую с помощью калмановской фильтрации; дисперсия в оценке позиции показана с помощью овалов (а); результаты калмановского сглаживания для той же последовательности результатов наблюдения (б) Мы можем вывести не только уравнения фильтрации с помощью линейных гауссовых моделей, но и уравнения сглаживания. Результаты сглаживания показаны на рис. 15.7,5. Обратите внимание на то, как резко сокращается дисперсия в оценке позиции, за исключением концов траектории (объясните, почему), и насколько более гладкой становится оцениваемая траектория.
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|