Выше было описано несколько вариантов применения алгоритма ЕМ. Каждый из них сводился к тому, что вычислялись ожидаемые значения скрытых переменных для каждого примера, а затем повторно вычислялись параметры с использованием ожидаемых значений так, как если бы они были наблюдаемыми значениями. Допустим, что χ — все наблюдаемые значения во всех примерах, и предположим, что ζ обозначает все скрытые переменные для всех примеров, а θ представляет собой все параметры для модели вероятности. В таком случае алгоритм ЕМ можно представить с помощью следующего уравнения:

Это уравнение составляет саму суть алгоритма ЕМ. При этом Ε-шаг сводится к вычислению выражения для суммы, которая представляет собой ожидаемое значение логарифмического правдоподобия "дополненных" данных по отношению к распределению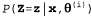, т.е. распределение апостериорных вероятностей по скрытым переменным при наличии полученных данных. С другой стороны, М-шаг представляет собой максимизацию этого ожидаемого логарифмического правдоподобия по отношению к параметрам. При использовании смешанного гауссова распределения скрытыми переменными являются, гдеравна 1, если пример j был сформирован компонентом i. При использовании байесовских сетей скрытые переменные представляют собой значения ненаблюдаемых переменных для каждого примера. При использовании скрытых марковских моделей скрытые переменные являются переходами. Начиная с этой общей формы, можно вывести алгоритм ЕМ для конкретного приложения, как только определены соответствующие скрытые переменные.

Поняв основную идею алгоритма ЕМ, можно легко вывести все возможные его варианты и усовершенствования. Например, во многих случаях Ε-шаг (вычисление распределений апостериорных вероятностей по скрытым переменным) является трудновыполнимым, как при использовании больших байесовских сетей. Оказалось, что в этом случае можно применить приближенный Ε-шаг и все еще получить эффективный алгоритм обучения. А если используется такой алгоритм формирования выборки, как МСМС (см. раздел 14.5), то процесс обучения становится полностью интуитивно понятным: каждое состояние (конфигурация скрытых и наблюдаемых переменных), посещенное алгоритмом МСМС, рассматривается точно также, как если бы оно было полным наблюдением. Поэтому параметры могут обновляться непосредственно после каждого перехода из состояния в состояние в алгоритме МСМС. Для определения с помощью обучения параметров очень больших сетей показали свою эффективность и другие формы приближенного вероятностного вывода, такие как вариационные и циклические методы.