|
Страница 3 из 5 Таким образом, если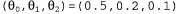 , то , то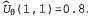 По результатам некоторой совокупности попыток будет получено множество выборочных значений По результатам некоторой совокупности попыток будет получено множество выборочных значений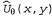 , после чего можно найти соответствие, наилучшее с точки зрения минимизации квадратичных ошибок, с помощью стандартной линейной регрессии (см. главу 20). , после чего можно найти соответствие, наилучшее с точки зрения минимизации квадратичных ошибок, с помощью стандартной линейной регрессии (см. главу 20). Применительно к обучению с подкреплением больше смысла имеет использование алгоритма оперативного обучения, который обновляет параметры после каждой попытки. Предположим, что осуществляется некоторая попытка, и суммарное вознаграждение, полученное начиная с квадрата (1,1), составляет 0.4. Такой результат наводит на мысль, что значение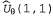 , составляющее в настоящее время 0.8, слишком велико и должно быть уменьшено. Как следует откорректировать параметры, чтобы добиться такого уменьшения? Как и в случае с обучением нейронной сети, запишем функцию ошибки и вычислим ее градиент по отношению к параметрам. Если , составляющее в настоящее время 0.8, слишком велико и должно быть уменьшено. Как следует откорректировать параметры, чтобы добиться такого уменьшения? Как и в случае с обучением нейронной сети, запишем функцию ошибки и вычислим ее градиент по отношению к параметрам. Если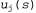 — наблюдаемое суммарное вознаграждение, полученное от состояния s и дальше, вплоть до j-й попытки, то ошибка определяется как (половина) квадратов разностей прогнозируемой общей суммы и фактической общей суммы: — наблюдаемое суммарное вознаграждение, полученное от состояния s и дальше, вплоть до j-й попытки, то ошибка определяется как (половина) квадратов разностей прогнозируемой общей суммы и фактической общей суммы: 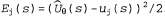 . Скорость изменения ошибки по отношению к каждому параметру . Скорость изменения ошибки по отношению к каждому параметру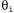 равна равна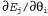 , поэтому, чтобы изменить значение параметра в направлении уменьшения ошибки, необходимо вычислить следующее выражение: , поэтому, чтобы изменить значение параметра в направлении уменьшения ошибки, необходимо вычислить следующее выражение:
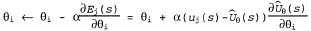 (21.10) (21.10)
Это выражение называется правилом Видроу—Хоффа, или дельта-правилом для оперативного вычисления по методу наименьших квадратов. Применительно к линейному аппроксиматору функции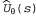 в уравнении 21.9 получаем три простых правила обновления: в уравнении 21.9 получаем три простых правила обновления: 
Эти правила можно применить к примеру, в котором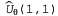 равно 0.8, а равно 0.8, а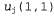 равно 0.4. Все значения равно 0.4. Все значения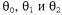 уменьшаются на коэффициент 0 . 4а, который уменьшает ошибку, относящуюся к квадрату (1,1). Обратите внимание на то, что изменение значений уменьшаются на коэффициент 0 . 4а, который уменьшает ошибку, относящуюся к квадрату (1,1). Обратите внимание на то, что изменение значений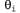 приводит также к изменению значений приводит также к изменению значений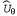 для всех прочих состояний! Именно это подразумевалось в приведенном выше утверждении, что функциональная аппроксимация позволяет агенту, проводящему обучение с подкреплением, обобщать свой опыт. для всех прочих состояний! Именно это подразумевалось в приведенном выше утверждении, что функциональная аппроксимация позволяет агенту, проводящему обучение с подкреплением, обобщать свой опыт.
|