А что подразумевается под системой, которая "не является гладкой" или "поведение которой неустойчиво"? Формально под этим подразумевается, что отклик системы в области, "близкой" (согласно ковариации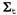) к текущему среднему , показывает существенную нелинейность. Чтобы понять суть этого описания неформально, рассмотрим пример слежения за птицей, которая летит через джунгли. Иногда создается впечатление, что птица направляется на высокой скорости прямо на ствол дерева. Фильтр Калмана (обычный или расширенный) позволяет получить только гауссово предсказание местонахождения птицы, притом что среднее соответствующего гауссова распределения будет находиться напротив центра ствола, как показано на рис. 15.8, а. Но более приемлемая модель полета птицы, с другой стороны, должна предсказывать ее действия по уклонению от удара об ствол путем поворота в одну сторону или в другую, как показано на рис. 15.8, б. Такая модель является в высшей степени нелинейной, поскольку птица принимает решение по уклонению от удара внезапно, в зависимости от того, где именно она находится по отношению к стволу.

Очевидно, что для работы с примерами, подобными этому, требуется более выразительный язык представления поведения моделируемой системы. В сообществе специалистов по теории управления, для которых в таких задачах, как маневры самолета по предотвращению столкновения, возникают аналогичные сложности, разработан стандартный подход — переключательные фильтры Калмана. В этом подходе предусмотрена одновременная эксплуатация нескольких фильтров Калмана, в каждом из которых используются разные модели систем, например, в одном из них моделируется прямой полет, в другом — резкий поворот налево, а в третьем — резкий поворот направо. При этом используется взвешенная сумма предсказаний, где вес зависит от того, насколько полно данные каждого фильтра совпадают с текущими данными. Как показано в следующем разделе, такой подход представляет собой частный случай общей модели динамической байесовской сети, созданной путем введения дискретной переменной состояния "маневра" в сеть, показанную на рис. 15.5. Переключательные фильтры Калмана рассматриваются дополнительно в упр. 15.5.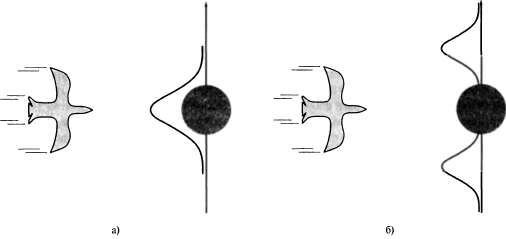

Рис. 15.8. Пример с птицей, летящей прямо на дерево (вид сверху): фильтр Калмана предсказывает местонахождение птицы с использованием единственного гауссова распределения, центр которого находится напротив препятствия (а); более реалистичная модель допускает выполнение птицей действия по уклонению от столкновения с препятствием, предсказывая, что птица облетит препятствие с одной стороны или с другой (б)