|
Страница 1 из 2 Расширим полное совместное распределение, приведенное в табл. 13.2, введя четвертую переменную, Weather. После этого полное совместное распределение, состоящее из 32 элементов (поскольку переменная Weather имеет четыре значения), принимает вид Ρ (Toothache, Catch, Cavity, Weather). Оно содержит четыре варианта таблицы, показанной в табл. 13.2, по одному на каждый вид погоды. Напрашивается резонный вопрос о том, какую связь имеют эти варианты друг с другом и с первоначальной таблицей, состоящей из трех переменных. Например, как связаны друг с другом высказывания Р( toothache, catch, cavity, Weather= cloudy) и P( toothache, catch, cavity) ? Один из способов получения ответа на этот вопрос состоит в использования правила произведения: 
Но человек, не верящий в существование колдунов, не может себе представить, что чьи-то проблемы с зубами могут влиять на погоду. Поэтому кажется резонным следующее утверждение:  (13.7) (13.7)
На основании этого можно вывести следующее: 
Аналогичное уравнение существует для каждого элемента в распределении Р (Toothache, Catch, Cavity, Weather). В действительности можно записать такое общее уравнение: 
Таким образом, 32-элементная таблица для четырех переменных может быть сконструирована из одной 8-элементной таблицы и одной 4-элементной. Такая декомпозиция показана схематически на рис. 13.1, а. Свойство вероятностей, используемое при составлении уравнения 13.7, называется ^ независимостью (а также маргинальной независимостью и абсолютной независимостью). В частности, погода независима от чьих-то проблем с зубами. Независимость между высказываниями а и b может быть показана следующим образом: 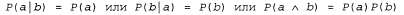 (13.8) (13.8)
 Рис. 13.1. Два примера факторизации большого совместного распределения на меньшие распределения с использованием свойства абсолютной независимости: независимы друг от друга погода и проблемы с зубами (а); независимы друг от друга броски монеты (б)
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|