Все эти формы записи являются эквивалентными. Свойство независимости между переменными х и Υ можно сформулировать следующим образом (все эти формы записи также эквивалентны):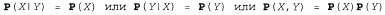

Утверждения о независимости обычно основаны на знаниях о проблемной области. Как показывает приведенный выше пример, эти утверждения позволяют существенно уменьшить объем информации, необходимой для описания полного совместного распределения. Если все множество переменных может быть разделено на независимые подмножества, то полное совместное распределение может быть фак-торизовано на отдельные совместные распределения, заданные на этих подмножествах. Например, совместное распределение результатов η независимых бросков монеты,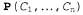, может быть представлено как произведение η распределений 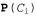с одной переменной. Например, с точки зрения практики очень благоприятным фактором является независимость данных зубоврачебного дела и метеорологии, поскольку в противном случае для занятия зубоврачебным делом потребовались бы глубокие знания в области метеорологии, и наоборот.

Поэтому утверждения о независимости, если они имеются, позволяют сократить размеры представления проблемной области и уменьшить сложность проблемы вывода. К сожалению, чистое разделение целых множеств переменных по признаку независимости встречается редко. Если между двумя переменными существует хоть какая-то связь, пусть даже косвенная, свойство независимости перестает соблюдаться. Кроме того, даже независимые подмножества могут оказаться чрезвычайно большими, например, в области стоматологии могут встретиться десятки заболеваний и сотни симптомов, причем все они взаимосвязаны друг с другом. Чтобы справиться с такими проблемами, мы должны иметь более тонкие методы, чем прямолинейная концепция независимости.