Окончательная модель, параметры которой определены в процессе обучения с помощью алгоритма ЕМ, применяемого к данным, приведенным на рис. 20.8, я, показана на рис. 20.8, в; она практически не отличается от первоначальной модели, на основе которой были сформированы данные. На рис. 20.9, а показан график изменения логарифмического правдоподобия данных, соответствующих текущей модели, которое изменяется в процессе выполнения алгоритма ЕМ. На этом графике заслуживают внимания две особенности. Во-первых, логарифмическое правдоподобие модели, окончательно полученной в процессе обучения, немного превышает соответствующее значение для первоначальной модели, на основании которой были сформированы исходные данные. Это явление может на первый взгляд показаться удивительным, но оно просто отражает тот факт, что данные были сформированы случайным образом, поэтому существует вероятность того, что они не являются точным отражением самой базовой модели. Во-вторых, любопытно то, что в алгоритме ЕМ логарифмическое правдоподобие данных повышается после каждой итерации. Можно доказать, что такова общая особенность данного алгоритма. Кроме того, можно доказать, что при определенных условиях алгоритм ЕМ достигает локального максимума правдоподобия (а в редких случаях он может достичь точки перегиба или даже локального минимума). В этом смысле алгоритм ЕМ напоминает алгоритм восхождения к вершине с учетом градиента, но заслуживает внимания то, что в нем уже не применяется параметр со "ступенчатым изменением величины"!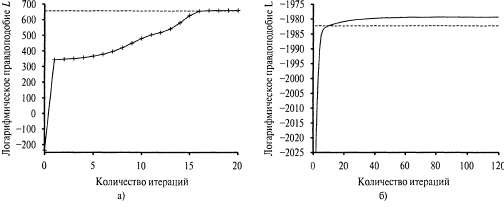

Рис. 20.9. Графики, показывающие изменение логарифмического правдоподобия данных, L, как функции от количества итераций ЕМ. Горизонтальная линия соответствует логарифмическому правдоподобию истинной модели: график для модели смешанного гауссова распределения, показанной на рис. 20.8 (а); график для байесовской сети, приведенной на рис. 20.10, а (б)

Но события не всегда развиваются так удачно, как можно было бы судить на основании рис. 20.9, а. Например, может случиться так, что один компонент гауссова распределения сузится настолько, что будет охватывать лишь единственную точку данных. В таком случае его дисперсия достигнет нуля, а правдоподобие увеличится до бесконечности! Еще одна проблема состоит в том, что может произойти "слияние" двух компонентов, в результате чего они примут одинаковые значения средних и дисперсий, а точки данных станут для них общими. Вырожденные локальные максимумы такого рода представляют собой серьезную проблему, особенно в случае большого количества измерений. Одно из решений состоит в наложении распределений априорных вероятностей на параметры модели и применении версии MAP алгоритма ЕМ. Еще одно решение состоит в перезапуске вычислений для некоторого компонента с новыми случайно выбранными параметрами, если он становится слишком малым или слишком близким к другому компоненту. Иногда имеет также смысл выбирать для инициализации параметров более обоснованные значения.