Оценки плотности, подобные приведенным на рис. 20.13, определяют совместные распределения по пространству входных данных. Но в отличие от байесовской сети, представление на основе экземпляра не может содержать скрытых переменных, а это означает, что может выполняться неконтролируемая кластеризация, как это было в случае с моделью смешанного гауссова распределения. Тем не менее оценка плотности все еще может использоваться для предсказания целевого значения у по входным значениям характеристики χ путем вычисления вероятности P(y|x)=p(y,х)/Р(х), при условии, что обучающие данные включают значения для соответствующей целевой характеристики.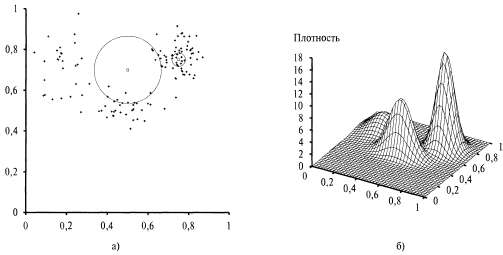

Рис. 20.12. Пример применения оценки плотности с к ближайшими соседними точками: частичная выборка данных, показанных на рис. 20.8, а, состоящая из 128 точек, наряду с двумя точками запроса и их окрестностями, которые включают 10 ближайших соседних точек (а); трехмерный график смешанного гауссова распределения, на основании которого были получены эти данные (б)

Рис. 20.13. Результаты применения метода оценки плотности с использованием окрестностей, включающих к ближайших соседних точек, к данным, приведенным на рис. 20.12, а, при к=3, 10 и 4 0 соответственно

Идею оценки характеристик с помощью ближайшей соседней точки можно также непосредственно использовать в контролируемом обучении. Если имеется проверочный пример с входными данными х, то выходное значение y=h(x) можно получить на основании значений у для к ближайших соседних точек точки х. В дискретном случае единственное предсказание можно получить с помощью мажоритарного голосования, а в непрерывном случае — предусмотреть усреднение по к значениям или применить локальную линейную регрессию, подгоняя гиперплоскость к к точкам и предсказывая значение в точке x с помощью этой гиперплоскости.