|
Страница 3 из 4 Таким образом, процесс обратного распространения можно кратко описать, как показано ниже. • Вычислить значения Δ для выходных элементов с использованием наблюдаемой ошибки. • Начиная с выходного слоя, повторять следующие действия для каждого слоя в сети до тех пор, пока не будет достигнут самый первый скрытый слой: • распространять значения Δ обратно к предыдущему слою; • обновлять веса между этими двумя слоями. Подробный алгоритм приведен в листинге 20.2. Листинг 20.2. Алгоритм обратного распространения для обучения в многослойных сетях 
Теперь исходя из основных принципов выведем уравнения обратного распространения к радости читателей, интересующихся математикой. Квадратичная ошибка на одном примере определяется следующим образом: 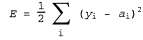
где сумма вычисляется по всем узлам выходного слоя. Чтобы определить градиент по отношению к конкретному весу в выходном слое, достаточно развернуть только выражение для активации в выходном слое, достаточно развернуть только выражение для активации , поскольку все другие термы в этой операции суммирования не зависят от , поскольку все другие термы в этой операции суммирования не зависят от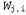 : : 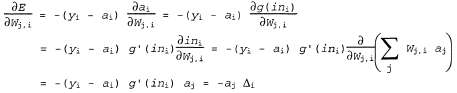
где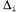 определено, как указано выше. Чтобы получить градиент по отношению к весам определено, как указано выше. Чтобы получить градиент по отношению к весам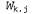 связей, соединяющих входной слой со скрытым слоем, необходимо по-прежнему вычислять всю сумму по i, поскольку изменение в значениях связей, соединяющих входной слой со скрытым слоем, необходимо по-прежнему вычислять всю сумму по i, поскольку изменение в значениях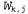 могут повлиять на каждое выходное значение могут повлиять на каждое выходное значение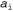 . При этом придется также развертывать выражение для активаций . При этом придется также развертывать выражение для активаций . Ниже показан ход вывода формулы во всех подробностях, поскольку любопытно понаблюдать за тем, как оператор производной распространяется в обратном направлении через сеть: . Ниже показан ход вывода формулы во всех подробностях, поскольку любопытно понаблюдать за тем, как оператор производной распространяется в обратном направлении через сеть: 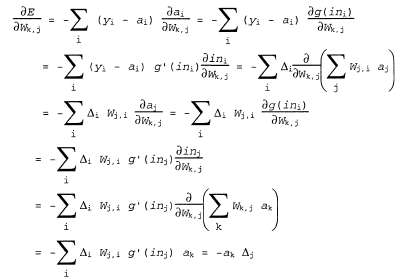
где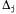 определено, как показано выше. Таким образом, получено то же правило обновления, которое было сформулировано выше на основании интуитивных соображений. Очевидно также, что этот процесс может быть продолжен применительно к сетям, имеющим больше одного скрытого слоя, и это соображение является обоснованием для общего алгоритма, приведенного в листинге 20.2. определено, как показано выше. Таким образом, получено то же правило обновления, которое было сформулировано выше на основании интуитивных соображений. Очевидно также, что этот процесс может быть продолжен применительно к сетям, имеющим больше одного скрытого слоя, и это соображение является обоснованием для общего алгоритма, приведенного в листинге 20.2.
|