|
Страница 2 из 4 Алгоритмы обучения для многослойных сетей подобны алгоритму обучения для персептронов, приведенному в листинге 20.1. Одно небольшое различие состоит в том, что может быть предусмотрено несколько выходов, поэтому должен применяться вектор выходов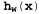 , а не одно значение, и с каждым примером должен быть связан вектор выходов у. Между этими алгоритмами существует также важное различие, которое заключается в том, что ошибка , а не одно значение, и с каждым примером должен быть связан вектор выходов у. Между этими алгоритмами существует также важное различие, которое заключается в том, что ошибка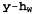 в выходном слое является очевидной, а ошибка в скрытых слоях кажется неуловимой, поскольку в обучающих данных отсутствует информация о том, какие значения должны иметь скрытые узлы. Как оказалось, можно обеспечить обратное распространение ошибки из выходного слоя в скрытые слои. Процесс обратного распространения может быть организован непосредственно на основе исследования общего градиента ошибки. Вначале мы опишем этот процесс на основе интуитивных представлений, а затем приведем его обоснование. в выходном слое является очевидной, а ошибка в скрытых слоях кажется неуловимой, поскольку в обучающих данных отсутствует информация о том, какие значения должны иметь скрытые узлы. Как оказалось, можно обеспечить обратное распространение ошибки из выходного слоя в скрытые слои. Процесс обратного распространения может быть организован непосредственно на основе исследования общего градиента ошибки. Вначале мы опишем этот процесс на основе интуитивных представлений, а затем приведем его обоснование. Рис. 20.23. Многослойная нейронная сеть с одним скрытым слоем и 10 входами, применимая для решения задачи с рестораном Правило обновления весов, применяемое в выходном слое, идентично уравнению 20.12. Предусмотрено несколько выходных элементов, поэтому предположим, что является i-м компонентом вектора ошибки является i-м компонентом вектора ошибки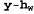 . Авторы находят также удобным определить модифицированную ошибку . Авторы находят также удобным определить модифицированную ошибку , с помощью которой правило обновления весов можно преобразовать следующим образом: , с помощью которой правило обновления весов можно преобразовать следующим образом:  (20.14) (20.14)
Чтобы обновить веса связей между входными и скрытыми элементами, необходимо определить величину, аналогичную терму ошибки для выходных узлов. Именно в этом и заключается суть метода обратного распространения ошибки. Идея его состоит в том, что скрытый узел j "отвечает" за некоторую долю ошибки в каждом из выходных узлов, с которыми он соединен. Таким образом, значения в каждом из выходных узлов, с которыми он соединен. Таким образом, значения разделяются в соответствии с весом связи между скрытым узлом и выходным узлом и распространяются обратно, обеспечивая получение значений разделяются в соответствии с весом связи между скрытым узлом и выходным узлом и распространяются обратно, обеспечивая получение значений для скрытого слоя. Правило распространения для значений для скрытого слоя. Правило распространения для значений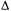 состоит в следующем: состоит в следующем:  (20.15) (20.15)
Теперь правило обновления весов между входными элементами и элементами скрытого слоя становится почти идентичным правилу обновления для выходного слоя: 
|