Кроме того, в этой логике могут быть реализованы простые "рефлекторные" варианты поведения с помощью импликационных высказываний с кванторами. Например, может быть предусмотрено следующее правило: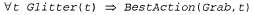

При наличии результатов восприятия и правил, приведенных в предыдущих абзацах, применение данного правила привело бы к желаемому заключению BestAction {Grab, 5) о том, что в данный момент следует выполнить действие Grab. Обратите внимание на соответствие между этим правилом и прямым соединением "восприятие/действие" в агенте на основе логической схемы, приведенной на рис. 7.9; соединение в этой логической схеме неявно предусматривает применение квантора к переменной, обозначающей время.

До сих пор в этом разделе все высказывания, касающиеся времени, были синхронными (т.е. "одновременными") высказываниями; это означает, что они связывали свойства некоторого состояния мира с другими свойствами того же состояния мира. А высказывания, которые допускают формирование "разновременных" рассуждений, называются диахронными; например, агенту требуется знать, как комбинировать информацию о его предыдущем местонахождении с информацией о только что выполненном действии, чтобы определить свое текущее местонахождение. Отложим обсуждение диахронных высказываний до главы 10, а пока будем просто предполагать, что в отношении предикатов, касающихся изменения местонахождения, и других предикатов, зависящих от времени, выполняется требуемый логический вывод.

Выше были представлены восприятия и действия; теперь настало время представить саму среду. Начнем с объектов. Очевидными кандидатами являются квадраты, ямы и вампус. Можно было бы присвоить имя каждому квадрату (и т.д.), но тогда тот факт, что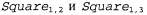являются соседними, пришлось бы оформить как "дополнительный" факт и нам потребовалось по одному такому факту для каждой пары квадратов. Поэтому лучше использовать сложный терм, в котором строка и столбец показаны в виде целых чисел; например, списковый терм [1,2]. В таком случае определение понятия соседства любых двух квадратов можно представить следующим образом: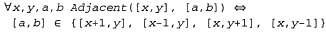