Второе важное семейство алгоритмов планирования пути основано на идее скелетирования. Эти алгоритмы сводят свободное пространство робота к одномерному представлению, для которого задача планирования становится проще. Такое представление с меньшим количеством измерений называется скелетом пространства конфигураций.

Пример применения метода скелетирования приведен на рис. 25.15: это — линия Вороного для свободного пространства, которая представляет собой геометрическое место всех точек, равноудаленных от двух или нескольких препятствий. Для того чтобы осуществить планирование пути с помощью линии Вороного, робот вначале переходит из текущей конфигурации в точку на линии Вороного. Можно легко показать, что такую операцию всегда можно выполнить с помощью передвижения по прямой в пространстве конфигураций. Затем робот следует по линии Вороного до тех пор, пока не достигнет точки, ближайшей к целевой конфигурации. Наконец, робот покидает линию Вороного и движется к цели. И на этом последнем этапе снова выполняется движение по прямой в пространстве конфигураций.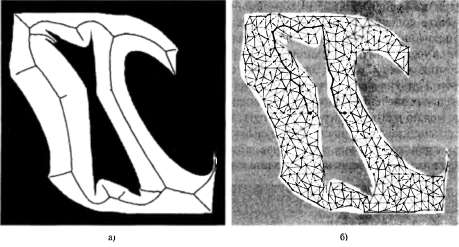

Рис. 25.15. Один из примеров метода скелетирования: линия Вороного — это геометрическое место точек, равноудаленных от двух или нескольких препятствий в пространстве конфигураций (а); вероятностная дорожная карта, состоящая из 400 случайно выбранных точек в свободном пространстве (б)

Таким образом, первоначальная задача планирования пути сводится к поиску пути на линии Вороного, которая обычно является одномерной (за исключением некоторых частных случаев) и имеет конечное количество таких точек, в которых пересекаются три или большее количество одномерных кривых. Поэтому задача поиска кратчайшего пути вдоль линии Вороного сводится к задаче поиска в дискретном графе такого же типа, как было описано в главах 3 и 4. Движение по линии Вороного может не обеспечить получение кратчайшего пути, но обнаруженные пути будут отличаться наличием максимальных расстояний от препятствий. Недостатки методов, основанных на использовании линии Вороного, состоят в том, что их сложно применять в пространствах конфигураций с большими размерностями, кроме того, при их использовании приходится совершать слишком большие обходные маневры, если пространство конфигураций характеризуется широким размахом. К тому же может оказаться сложным вычисление линии Вороного, особенно в пространстве конфигураций, характеризующемся сложной формой препятствий.