В данном случае алгоритм Prior-Sample возвращает событие [ true, false, true, true].

Можно легко показать, что алгоритм Prior-Sample формирует выборки на основе априорного совместного распределения, которое задано рассматриваемой сетью. Прежде всего предположим, что представляет собой вероятность того, что конкретное событие сформировано алгоритмом Prior-Sample. Достаточно лишь проанализировать сам процесс формирования выборки, чтобы убедиться в справедливости следующего соотношения, поскольку каждый этап формирования выборки зависит только от значений родительских переменных: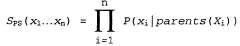

Это выражение должно показаться читателю весьма знакомым, поскольку оно определяет также вероятность события в соответствии с представлением совместного распределения в байесовской сети, как указано в уравнении 14.1. Поэтому получаем следующее: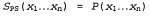

Благодаря такому простому факту задача получения ответов на вопросы с помощью выборок решается очень просто.

В любом алгоритме формирования выборки ответы вычисляются путем подсчета фактически сформированных выборок. Предположим, что общее количество выборок равно N, а также допустим, что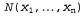— частота конкретного события . Следует полагать, что эта частота сойдется в пределе к ее ожидаемому значению, соответствующему вероятности сформированной выборки:

(14.4)

Например, рассмотрим событие, полученное ранее: [true, false, true, true]. Вероятность формирования выборки для этого события такова: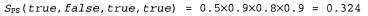

Поэтому следует полагать, что в пределе, при очень больших значениях N, около 32,4% выборок будут относиться к этому событию.

В последующем изложении мы будем использовать знак приближенного равенствадля обозначения соотношения, имеющего именно этот смысл, — что оцениваемая вероятность становится точной при больших пределах количества выборок. Такая оценка называется согласованной. Например, может быть получена согласованная оценка вероятности любого частично заданного события, где , следующим образом:

(14.5)

Это означает, что вероятность события можно оценить с помощью деления количества выборок частично заданного события на количество всех событий, полученных в процессе формирования выборок. Например, если на основании сети с описанием опрыскивателя (см. рис. 14.9, а) сформирована 1000 выборок и для 511 из них справедливо выражение Rain=true, то оценка вероятности дождя, которая записывается как, равна 0,511.