|
Страница 2 из 4 Чтобы найти подход к решению задач POMDP, необходимо вначале определить их должным образом. Любая задача POMDP состоит из таких же компонентов, как и задача MDP (модель перехода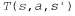 и функция вознаграждения R(s)), но имеет также модель наблюдения 0(s, о), которая задает вероятность получения результатов наблюдения о в состоянии3 s. Например, рассматриваемый в данном случае агент без датчиков имеет только одно возможное наблюдение (пустое наблюдение), и такое наблюдение возникает с вероятностью 1 в любом состоянии. и функция вознаграждения R(s)), но имеет также модель наблюдения 0(s, о), которая задает вероятность получения результатов наблюдения о в состоянии3 s. Например, рассматриваемый в данном случае агент без датчиков имеет только одно возможное наблюдение (пустое наблюдение), и такое наблюдение возникает с вероятностью 1 в любом состоянии. В главах 3 и 12 рассматривались задачи планирования в недетерминированных и частично наблюдаемых вариантах среды и было определено доверительное состояние (множество фактических состояний, в которых может находиться агент) как ключевая концепция для описания и вычисления решений. В задачах POMDP это понятие требует определенного уточнения. Теперь доверительным состоянием b становится распределение вероятностей по всем возможным состояниям. Например, начальное доверительное состояние в ситуации, показанной на рис. 17.6, а, может быть записано как 
Мы будем обозначать через b(s) вероятность, присвоенную фактическому состоянию s доверительным состоянием b. Агент может вычислить свое текущее доверительное состояние как распределение условных вероятностей по фактическим состояниям, если дана последовательность происшедших до сих пор наблюдений и действий. Такая задача по сути сводится к задаче фильтрации (см. главу 15). Основное рекурсивное уравнение фильтрации (см. уравнение 15.3) показывает, как вычислить новое доверительное состояние из предыдущего доверительного состояния и нового наблюдения. Для решения задач POMDP необходимо также учитывать определенное действие и использовать немного другую систему обозначений, но результат остается по сути тем же самым. Если предыдущим доверительным состоянием было b(s), а агент выполнил действие а и получил результаты наблюдения о, то новое доверительное состояние определяется следующим соотношением: 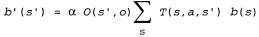 (17.11) (17.11)
где α — нормализующая константа, при использовании которой сумма вероятностей доверительных состояний становится равной 1. Это уравнение можно сокращенно записать как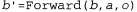
|