|
Страница 4 из 4 На рис. 25.8 показано применение понятия линеаризации для (одномерной) модели движения робота. В левой части показана нелинейная модель движения 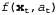 (параметр (параметр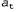 на этом графике не показан, поскольку он не играет никакой роли в этой линеаризации). В правой части эта функция аппроксимируется линейной функцией на этом графике не показан, поскольку он не играет никакой роли в этой линеаризации). В правой части эта функция аппроксимируется линейной функцией . График этой линейной функции проходит по касательной к кривой f в точке . График этой линейной функции проходит по касательной к кривой f в точке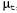 , которая определяет среднюю оценки состояния во время t. Такая линеаризация называется разложением в рад Тейлора (первой степени). Фильтр Кал-мана, линеаризующий функции f и h с помощью разложения в ряд Тейлора, называется расширенным фильтром Калмана (или Extended Kalman Filter— EKF). На рис. 25.9 показана последовательность оценок, полученных роботом, который действует под управлением алгоритма локализации на основе расширенного фильтра Калмана. По мере передвижения робота неопределенность в оценке его местонахождения возрастает, как показано с помощью эллипсов погрешностей. Но как только робот начинает получать данные о дальности и азимуте до отметки с известным местонахождением, его погрешность уменьшается. Наконец, погрешность снова возрастает, как только робот теряет отметку из виду. Алгоритмы EKF действуют успешно, если отметки являются легко идентифицируемыми. Еще один вариант состоит в том, что распределение апостериорных вероятностей может быть мультимодальным, как показано на рис. 25.7, б. Задача, для решения которой требуется знать идентификацию отметок, представляет собой пример задачи ассоциации данных, которая обсуждалась в конце главы 15. , которая определяет среднюю оценки состояния во время t. Такая линеаризация называется разложением в рад Тейлора (первой степени). Фильтр Кал-мана, линеаризующий функции f и h с помощью разложения в ряд Тейлора, называется расширенным фильтром Калмана (или Extended Kalman Filter— EKF). На рис. 25.9 показана последовательность оценок, полученных роботом, который действует под управлением алгоритма локализации на основе расширенного фильтра Калмана. По мере передвижения робота неопределенность в оценке его местонахождения возрастает, как показано с помощью эллипсов погрешностей. Но как только робот начинает получать данные о дальности и азимуте до отметки с известным местонахождением, его погрешность уменьшается. Наконец, погрешность снова возрастает, как только робот теряет отметку из виду. Алгоритмы EKF действуют успешно, если отметки являются легко идентифицируемыми. Еще один вариант состоит в том, что распределение апостериорных вероятностей может быть мультимодальным, как показано на рис. 25.7, б. Задача, для решения которой требуется знать идентификацию отметок, представляет собой пример задачи ассоциации данных, которая обсуждалась в конце главы 15. 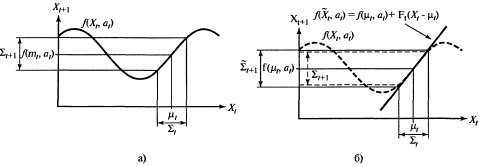 Рис. 25.8. Одномерная иллюстрация линеаризованной модели движения: функция f, проекция среднего и интервал ковариации (основанный на и интервал ковариации (основанный на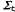 ) во время t+1 (а); линеаризованная версия представляет собой касательную к кривой функции f при значении ) во время t+1 (а); линеаризованная версия представляет собой касательную к кривой функции f при значении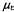 . Проекция среднего . Проекция среднего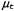 определена правильно. Однако проекция ковариации определена правильно. Однако проекция ковариации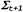 отличается от отличается от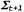 (б) (б) 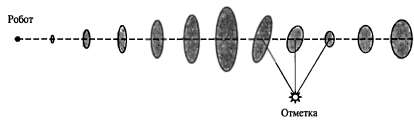
Рис. 25.9. Пример локализации с использованием расширенного фильтра Калмана. Робот движется по прямой. По мере его продвижения неопределенность постепенно возрастает, как показано с помощью эллипсов погрешностей. А после обнаружения роботом отметки с известной позицией неопределенность уменьшается
<< В начало < Предыдущая 1 2 3 4 Следующая > В конец >>
|