В данном разделе будет описан простой метод вероятностного вывода, т.е. вычисления апостериорных вероятностей для высказываний, заданных в виде запросов, на основании наблюдаемых свидетельств. Мы будем использовать полное совместное распределение как своего рода "базу знаний", из которой могут быть выведены ответы на все вопросы. В ходе этого мы также представим несколько полезных методов манипулирования уравнениями, в которых учитываются вероятности.

Начнем с очень простого примера — с описания проблемной области, состоящей только из трех булевых переменных, Toothache, Cavity и Catch (неприятные ощущения от захвата зуба стальными клещами дантиста все еще свежи в памяти автора). Полное совместное распределение представляет собой таблицу с размерами 2x2x2 (табл. 13.2).

Таблица 13.2. Полное совместное распределение для мира Toothache, Cavity, Catch

Обратите внимание на то, что вероятности в этом совместном распределении в сумме составляют 1, как и требуется согласно аксиомам вероятностей. Следует также отметить, что уравнение 13.2 предоставляет нам прямой способ вычисления вероятности любого высказывания, простого или сложного: мы должны определить те атомарные события, в которых данное высказывание является истинным, и сложить их вероятности. Например, имеется шесть атомарных событий, в которых истинным является высказывание cavity v toothache: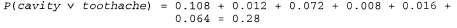

Одна из задач, которая встречается особенно часто, состоит в том, чтобы извлечь из подобной таблицы распределение вероятностей по некоторому подмножеству переменных или по одной переменной. Например, складывая элементы первого ряда табл. 13.2, получим безусловную, или .маргинальную, вероятность события cavity.

P(cavity) = 0.108 + 0.012 + 0.072 + 0.008 = 0.2

Такой процесс называется маргинализацией, или исключением из суммы, поскольку из суммы вероятностей исключаются прочие переменные, кроме Cavity. Можно записать следующее общее правило маргинализации для любых множеств переменных Υ и Z:

(13.4)