|
Страница 2 из 3 Это означает, что распределение вероятностей по Υ может быть получено путем исключения из суммы вероятностей всех прочих переменных, относящихся к любому совместному распределению вероятностей, содержащему Υ. В одном из вариантов этого правила учитываются условные вероятности, а не совместные вероятности с использованием правила произведения: 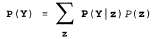 (13.5) (13.5)
Это правило называется правилом обусловливания. Как оказалось, правила маргинализации и обусловливания являются очень полезными правилами для всех видов логических выводов, в которых применяются вероятностные выражения. В большинстве случаев нас будет интересовать задача вычисления условных вероятностей некоторых переменных при наличии свидетельств, касающихся других переменных. Условные вероятности можно найти, вначале воспользовавшись уравнением 13.1 для получения выражения в терминах безусловных вероятностей, а затем рассчитав это выражение на основании полного совместного распределения. Например, можно вычислить вероятность наличия дупла после получения свидетельства о том, что пациент страдает от зубной боли, следующим образом: 
Просто для проверки мы можем также рассчитать вероятность того, что у пациента нет дупла, если у него наблюдается зубная боль: 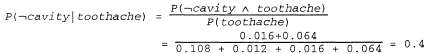
Обратите внимание на то, что в этих двух примерах вычисления вероятности терм 1/Р( toothache) остается постоянным, независимо от того, какое значение Cavity вычисляется. Фактически этот терм может рассматриваться как константа нормализации для распределения Ρ (Cavity|toothache), гарантирующая, что полученные вероятности в сумме составят 1. Во всех главах этой книги, где речь идет о вероятностях, для обозначения подобных констант будем использовать символ а. С помощью такого обозначения можно записать два приведенных выше уравнения в виде одного: 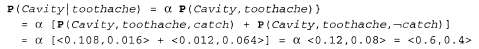
Как оказалось, нормализация является полезным сокращением во многих вероятностных вычислениях.
|