Здесь к переменной χ в атомарном высказывании Brother [Richard, χ) применяется квантор существования. Общее правило состоит в том, что переменная принадлежит к самому внутреннему квантору, в котором она упоминается; это означает, что такая переменная не может стать субъектом действия любого другого квантора7. Еще один способ анализа приведенного выше высказывания состоит в следующем:— это высказывание о Ричарде (о том, что у него есть брат), а не о переменной х, поэтому размещение квантораза пределами данного высказывания не оказывает на него никакого действия, и оно могло быть равным образом записано как. Но поскольку такая ситуация может стать источником путаницы, в подобных обстоятельствах мы всегда будем использовать разные переменные.

Связь между кванторами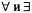

Кванторы V и 5 фактически тесно связаны друг с другом через отрицание. Утверждение о том, что никто не любит пастернак, равносильно утверждению о том, что не существует никого, кто бы его любил, и наоборот:

По такому же принципу может быть сформирована более сложная конструкция; например, выражение "Все любят мороженое" означает, что нет никого, кто не любил бы мороженое:

Поскольку квантор V фактически определяет в универсуме объектов конъюнкцию, а квантор 3 определяет дизъюнкцию, нет ничего удивительного в том, что они подчиняются правилам де Моргана. Правила де Моргана для высказываний с кванторами и без кванторов приведены ниже.

Таким образом, в действительности нет необходимости иметь одновременно кванторы V и 5, так же как фактически не нужны обе связки л и v. Тем не менее удобство для чтения важнее, чем экономия выразительных средств, поэтому мы будем пользоваться обоими этими кванторами.