Высказывание с квантором всеобщности 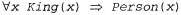является истинным при первоначальной интерпретации, если высказывание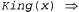 Person (x) истинно в каждой из пяти расширенных интерпретаций. Это означает, что данное высказывание с квантором всеобщности эквивалентно утверждению об истинности следующих пяти высказываний:

Рассмотрим внимательно это множество утверждений. Поскольку в нашей модели единственным королем является король Джон, то во втором высказывании утверждается, что он — человек, как и следовало ожидать. А что же можно сказать об остальных четырех высказываниях, в частности о тех, в которых приведены утверждения о ногах и коронах? Являются ли они частью смысла утверждения "Все короли являются людьми"? Действительно, остальные четыре утверждения истинны в данной модели, но не позволяют ничего судить о том, можно ли считать людьми ноги, короны или даже Ричарда. Это связано с тем, что ни один из этих объектов не является королем. Рассматривая истинностную таблицу для связки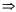(см. табл. 7.1), можно убедиться в том, что импликация истинна, даже если ее предпосылка ложна, независимо от того, является ли истинным заключение. Таким образом, утверждая истинность высказывания с квантором всеобщности, что эквивалентно утверждению об истинности целого списка отдельных импликаций, мы в конечном итоге утверждаем об истинности правила, выраженного в виде этого высказывания, только для тех объектов, для которых предпосылка является истинной, и вообще ничего не говорим о тех объектах, для которых предпосылка ложна. 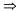Поэтому, как оказалось, записи истинностной таблицы, относящиеся к связке, являются идеальным способом формулировки общих правил с кванторами всеобщности.

Распространенная ошибка, которую часто допускают даже внимательные читатели, которые прочли предыдущий абзац несколько раз, состоит в том, что они используют конъюнкцию вместо импликации. Тогда следующее высказывание: