Четыре способа, с помощью которых три плоские поверхности могут быть соединены в одной вершине, показаны на рис. 24.15. Эти примеры могут быть также составлены путем разделения куба на восемь октантов. В таком случае различные возможные трехгранные вершины в центре куба создаются путем заполнения разных октантов. Вершина, обозначенная цифрой 1, соответствует одному заполненному октанту, вершина с цифрой 3 — трем заполненным октантам и т.д. Рекомендуем читателям самим убедиться в том, что на данном рисунке действительно представлены все возможности. Например, попытка заполнить два октанта в кубе не приводит к созданию допустимой трехгранной вершины в центре. Следует также отметить, что эти четыре случая соответствуют различным комбинациям выпуклых и вогнутых краев, которые встречаются в данной вершине.

Рис. 24.15. Четыре вида трехгранных вершин

Три края, встречающихся в вершине, делят окружающее пространство на восемь октантов. Вершина видна из любого октанта, не заполненного твердым материалом. Перемещение точки зрения в пределах одного октанта не приводит к получению изображения с различными типами соединений. Вершина, обозначенная цифрой 1 на рис. 24.15, может рассматриваться из любого из оставшихся семи октантов; при этом наблюдаются метки соединения, показанные на рис. 24.16.

Рис. 24.16. Изменение внешнего вида вершины, обозначенной цифрой 1 на рис. 24.15

Работа по составлению исчерпывающего списка различных способов, с помощью которых может рассматриваться каждая вершина, привела к получению вариантов, показанных на рис. 24.17. Получено четыре различных типа соединений, которые могут быть выделены на изображении: L-соединения, Y-соединения, стреловидные соединения и Т-соединения. L-соединения соответствуют двум видимым краям. Y-соединения и стреловидные соединения соответствуют результатам рассмотрения трех краев, но различие между ними состоит в том, что в Y-соединении ни один из трех углов не превышает 180°. Т-соединения связаны с закрытием одной поверхности другой. Если ближайшая, непрозрачная поверхность закрывает вид на дальше расположенный ее край, будет получен непрерывный край, который встречается с частично закрытым краем. Четыре метки Т-соединения соответствуют закрытию четырех различных типов краев.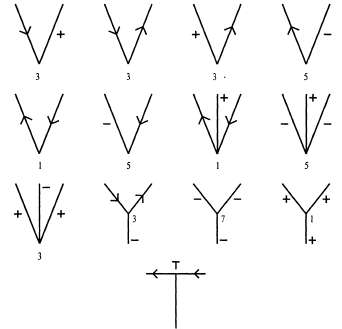

Рис. 24.17. Множество меток Хаффмена—Клоувса

При использовании этого словаря соединений во время поиска разметки для контурного рисунка приходится решать задачу определения того, какие интерпретации соединений являются глобально совместимыми. Соблюдение свойства совместимости обеспечивается путем применения правила, согласно которому каждой линии на рисунке вдоль всей ее длины должна быть присвоена одна и только одна метка. Вальц [1552] предложил алгоритм решения этой задачи (фактически применимый даже для расширенной ее версии с тенями, трещинами и разделимо вогнутыми краями), который стал одним из первых приложений метода удовлетворения ограничений в искусственном интеллекте (см. главу 5). В терминологии задач CSP переменными являются соединения, значениями— разметки для этих соединений, а ограничениями служит то, что каждая линия имеет единственную метку. Хотя задача разметки линии для сцен с трехфанными объектами является NP-полной, на практике стандартные алгоритмы CSP показали высокую производительность при их решении.