1.    Метки + и - представляют соответственно выпуклые и вогнутые края. Они связаны с поверхностными нормальными сосредоточенными неоднородно-стями, в которых видны обе поверхности, стыкующиеся вдоль этого края.

2.    Меткаили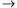представляет закрывающий выпуклый край. При просмотре сцены из видеокамеры обе конечные части поверхности, ограниченные замкнутой кривой, которые стыкуются вдоль этого края, лежат на одной и той же стороне, но одна из них закрывает другую. По мере перемещения по направлению стрелки эти закрывающие поверхности остаются справа.

3.    Меткаилипредставляет лимб. На этой линии поверхность плавно искривляется по кругу, закрывая саму себя. По мере перемещения в направлении, обозначенным двойной стрелкой, закрывающая поверхность остается справа. Луч зрения проходит по касательной к поверхности во всех точках лимба. По мере изменения точки зрения лимбы меняют свое положение на поверхности объекта.

Если количество линий на рисунке равно п, то количество вариантов присваивания меток линий, определяемое законами комбинаторики, равно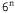, но количество физически возможных вариантов присваивания по сравнению с этим количеством составляет лишь очень небольшую величину. Задача определения таких возможных присваиваний меток называется задачей разметки линий. Следует отметить, что эта задача имеет смысл, только если метка остается одинаковой на всем протяжении линии. Но такое условие не всегда соблюдается, поскольку метки могут изменяться вдоль линий на изображениях выпукло-вогнутых криволинейных объектов. В настоящей главе для предотвращения указанных сложностей будут рассматриваться исключительно только многогранные объекты.

Хаффмен [702] и Клоувс [271] независимо друг от друга впервые предприняли попытку применить систематический подход к анализу сцен с многогранными объектами. В своем анализе Хаффмен и Клоувс ограничивались сценами с непрозрачными трехгранными твердыми телами; таковыми являются объекты, в которых в каждой вершине сходятся три и только три плоские поверхности. В случае наличия сцен с многочисленными объектами они, кроме этого, исключали такие выравнивания объектов, которые могли бы привести к нарушению предположения о наличии только трехгранных объектов, например сцен, в которых два куба имеют общий край. Не допускалось также наличие трещин (т.е. "краев", вдоль которых касательные плоскости являются непрерывными). Для такого мира трехгранных объектов Хаффмен и Клоувс подготовили исчерпывающий список всех различных типов вершин и описали всевозможные способы, с помощью которых эти вершины могут рассматриваться под общей точкой зрения. Условие, согласно которому должна существовать общая точка зрения, фактически гарантирует то, что если возникает небольшое движение глаза наблюдателя, ни одно из соединений плоскостей не меняет свой характер. Например, из этого условия следует, что если три линии пересекаются на изображении, то должны также пересекаться соответствующие края в сцене.