Очевидно, что в первые два дня решение выбрать дорогу В не лишено смысла, но в третий день ни один человек в здравом уме не выберет дорогу В. Однако именно такой вариант подсказывает метод усреднения по прогнозам: дорога В является оптимальной в ситуациях, возникающих в первый и второй дни, поэтому она оптимальна и в третий день, поскольку должна иметь место одна из двух предыдущих ситуаций. Вернемся к карточной игре: после того как игрок МАХ пойдет картой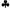9, игрок MIN заберет взятку картой10. Как и прежде, MIN пойдет с карты2, но теперь игрок МАХ окажется перед развилкой на дороге без каких-либо указаний. Если игрок МАХ выбросит карту6, а у игрока MIN все еще будет оставаться карта4, то эта карта4 станет козырной и игрок МАХ проиграет игру. Аналогичным образом, если игрок МАХ выбросит карту6, а у игрока MIN все еще будет оставаться карта4, игрок МАХ также проиграет. Поэтому игра с первым ходом картой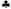9 ведет к ситуации, в которой игрок МАХ имеет 50%-ную вероятность проигрыша. (Для него было бы гораздо лучше вначале сыграть картами6 и. 6, гарантируя для себя ничейную игру.)

Из всего этого можно извлечь урок, что при недостатке информации игрок должен учитывать, какую информацию он будет иметь в каждый момент игры. Недостаток алгоритма, применяемого игроком МАХ, состоит в том, что в нем предполагается, будто при каждой возможной раздаче игра будет развиваться так, как если бы все карты оставались видимыми. Как показывает данный пример, это вынуждает игрока МАХ действовать таким образом, как будто неопределенность разрешится, когда настанет время. Кроме того, в алгоритме игрока МАХ никогда не принимается решение, что нужно собирать информацию (или предоставлять информацию партнеру), поскольку этого не требуется делать в рамках каждой отдельной раздачи; тем не менее в таких играх, как бридж, часто бывает целесообразно сыграть такой картой, которая помогла бы кое-что узнать о картах противника или сообщить партнеру о своих собственных картах. Такие стереотипы поведения формируются автоматически оптимальным алгоритмом ведения игр с неполной информацией. Подобный алгоритм выполняет поиск не в пространстве состояний мира (под этим подразумеваются карты, находящиеся на руках у игроков), а в пространстве доверительных состояний (представлений о том, кто какие карты имеет и с какими вероятностями). Авторы смогут объяснить этот алгоритм должным образом в главе 17 после разработки всего необходимого вероятностного инструментария. А в данной главе необходимо также остановиться на одном заключительном и очень важном замечании: в играх, с неполной информацией лучше всего выдавать противнику как можно меньше информации, а наилучший способ сделать это чаще всего состоит в том, чтобы действовать непредсказуемо. Вот почему санитарные врачи, посещая для проверки предприятия общественного питания, не сообщают заранее о своих визитах.