Обучение на основе объяснения базируется на том важном принципе, что вначале необходимо составить объяснение данного наблюдения с использованием априорных знаний, а затем сформировать определение класса случаев, для которого может использоваться такая же структура объяснения. Подобное определение может лечь в основу правила, охватывающего все случаи данного класса. Само "объяснение" может представлять собой логическое доказательство, но в более общем случае объяснением может служить любой процесс формирования рассуждений или решения задачи, этапы которого полностью определены. Ключом к успешному формированию объяснения является определение необходимых условий для того, чтобы такие же этапы процесса можно было применить к другому случаю.

Мы будем использовать в качестве рассматриваемой здесь системы формирования логических рассуждений простую систему доказательства теорем по методу обратного логического вывода, которая описана в главе 9. Дерево доказательства для случая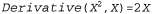слишком велико для того, чтобы его можно было использовать в качестве примера, поэтому для иллюстрации применяемого метода обобщения рассмотрим более простую задачу. Предположим, что задача состоит в том, чтобы упростить выражение 1х (0+Х). База знаний включает следующие правила:

Доказательство того, что ответом является х, приведено на рис. 19.5, сверху. В методе обучения на основе объяснения фактически одновременно формируются два дерева доказательства. Во втором дереве доказательства используется цель, описанная с помощью переменных, в которой константы первоначальной цели заменены переменными. По мере развития первоначального доказательства так же поэтапно развивается доказательство с помощью переменных, в котором применяются точно такие же приложения правил. Использование некоторых правил может вызвать конкретизацию определенных переменных. Например, для того чтобы можно было применить правило Rewri te( lxu, u), необходимо вначале связать с 1 переменную χ в подцели Rewrite (xx(y+z) , ν). Аналогичным образом, переменная у должна быть связана с 0 в подцели Rewri te(y+z,v' ), для того чтобы можно было использовать правило Rewrite(0+ и, и). После получения обобщенного дерева доказательства остается только взять листовые узлы (с необходимыми связываниями) и сформулировать общее правило для целевого предиката, следующим образом: