|
Предполагается, что эвристическая функция h(n) оценивает стоимость решения, начиная от состояния, связанного с узлом п. Как может некоторый агент составить подобную функцию? Одно из решений было приведено в предыдущем разделе, а именно: агент должен сформулировать ослабленные задачи, для которых может быть легко найдено оптимальное решение. Еще один подход состоит в том, что агент должен обучаться на основании полученного опыта. Здесь под "получением опыта" подразумевается, например, решение большого количества экземпляров игры в восемь. Каждое оптимальное решение задачи игры в восемь предоставляет примеры, на основе которых можно изучать функцию h (п). Каждый пример складывается из состояния, взятого из пути решения, и фактической стоимости пути от этой точки до решения. На основе данных примеров с помощью алгоритма индуктивного обучения может быть сформирована некоторая функция h(n), способная (при счастливом стечении обстоятельств) предсказывать стоимости решений для других состояний, которые возникают во время поиска. Методы осуществления именно такого подхода с использованием нейронных сетей, деревьев решения и других средств описаны в главе 18. (Применимы также методы обучения с подкреплением, которые рассматриваются в главе 21.) Методы индуктивного обучения действует лучше всего, когда в них учитываются характеристики состояния, релевантные для оценки этого состояния, а не просто общее описание состояния. Например, характеристика "количество стоящих не на своих местах фишек" может быть полезной при предсказании фактического удаления некоторого состояния от цели. Назовем эту характеристику х1(п). Например, можно взять 100 сформированных случайным образом конфигураций головоломки игры в восемь и собрать статистические данные об их фактических стоимостях решений. Допустим, это позволяет обнаружить, что при х1(п), равном 5, средняя стоимость решения составляет около 14, и т.д. Наличие таких данных позволяет использовать значение х1 для предсказания значений функции h(n). Безусловно, можно также применять сразу несколько характеристик. Второй характеристикой, 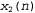 , может быть "количество пар смежных фишек, которые являются также смежными в целевом состоянии". Каким образом можно скомбинировать значения , может быть "количество пар смежных фишек, которые являются также смежными в целевом состоянии". Каким образом можно скомбинировать значения 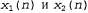 для предсказания значения h(n)? Общепринятый подход состоит в использовании линейной комбинации, как показано ниже. для предсказания значения h(n)? Общепринятый подход состоит в использовании линейной комбинации, как показано ниже. 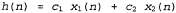
Константы с1 и с2 корректируются для достижения наилучшего соответствия фактическим данным о стоимостях решений. Предполагается, что константа с1 должна быть положительной, а с2 — отрицательной.
|