Теперь рассмотрим, в чем состоит ахиллесова пята языка Prolog: несогласованность между организацией поиска в глубину и деревьями поиска, которые включают повторяющиеся состояния и бесконечные пути. Рассмотрим следующую логическую программу, позволяющую определить, существует ли путь между двумя точками в ориентированном графе: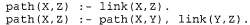

На рис. 9.5, а приведен простой граф, состоящий из трех узлов, который описан с помощью фактов link (a, b) и link (b, с). При использовании этой программы запрос path (а, с) вырабатывает дерево доказательства, показанное на рис. 9.6, а. С другой стороны, если эти два выражения расположены в таком порядке: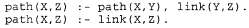

то система Prolog следует по бесконечному пути, как показано на рис. 9.6, б. Поэтому система Prolog является неполной, как и программа автоматического доказательства теоремы для определенных выражений (как показано в этом примере, даже применительно к программам, соответствующим формату языка Datalog), поскольку для некоторых баз знаний эта система оказывается неспособной доказать высказывания, которые из них следуют. Следует отметить, что алгоритм прямого логического вывода не подвержен этой проблеме: сразу после вывода фактов path (а, Ь), path (b, с) и path (а, с) процесс прямого логического вывода останавливается.

Обратный логический вывод с поиском в глубину сталкивается также с проблемами, обусловленными излишними вычислениями. Например, при поиске пути от узла А1 к узлу J4 на рис. 9.5, б система Prolog выполняет 877 этапов логического вывода, большинство из которых связано с поиском всех возможных путей к узлам, не позволяющим достичь цели. Такая проблема аналогична проблеме повторяющихся состояний, которая описывалась в главе 3. Общее количество этапов логического вывода может определяться экспоненциальной зависимостью от количества базовых фактов, вырабатываемых в процессе вывода. А если бы вместо этого применялся прямой логический вывод, то можно было бы ограничиться выработкой, самое большее, п2 фактов path (Χ, Υ), связывающих η узлов. При этом для решения задачи, приведенной на рис. 9.5, б, потребовалось бы только 62 этапа логического вывода.

Рис. 9.5. Иллюстрация недостатков языка Prolog: поиск пути от А до Сможет привести систему Prolog к созданию бесконечного цикла (а); граф, в котором каждый узел связан с двумя случайно выбираемыми преемниками на следующем уровне; для поиска пути от Αι до J4 требуется 877 этапов логического вывода (б)