В предыдущем разделе было показано, что возможно выработать оптимальную стратегию, даже если оценка функции полезности является неточной. Если очевидно, что одно действие лучше по сравнению со всеми остальными, то нет необходимости точно определять истинные значения величины полезности всех рассматриваемых состояний. Эта идея подсказывает альтернативный метод поиска оптимальных стратегий. В алгоритме итерации по стратегиям чередуются описанные ниже два этапа, начиная с некоторой исходной стратегии.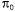

•    Оценка стратегии. На основе стратегиивычислить, полезность каждого состояния, если будет осуществлена стратегия.

•    Усовершенствование стратегии. Вычислить новую стратегиюс максимальной ожидаемой полезностью, используя прогноз на один шаг и исходя из значения(как в уравнении 17.4).

Алгоритм завершает свою работу после того, как этап усовершенствования стратегии не приводит к изменению значений полезности. Как известно, в этот момент функция полезностипредставляет собой фиксированную точку обновления Беллмана, поэтому является решением уравнений Беллмана, адолжна быть оптимальной стратегией. Поскольку для каждого конечного пространства состояний количество возможных стратегий является конечным и можно показать, что каждая итерация приводит к определению лучшей стратегии, то алгоритм итерации по стратегиям должен всегда завершать свою работу. Этот алгоритм показан в листинге 17.2.

Листинг 17.2. Алгоритм итерации по стратегиям для вычисления оптимальной стратегии

Очевидно, что этап усовершенствования стратегии является несложным, а как реализовать процедуру Policy-Evaluation? Оказалось, что осуществление такого подхода намного проще по сравнению с решением стандартных уравнений Беллмана (а именно это происходит в алгоритме итерации по значениям), поскольку действие, применяемое в каждом состоянии, зафиксировано в соответствии с выбранной стратегией. Стратегияопределяет действие, выполняемое в состоянии s на i-й итерации. Это означает, что можно воспользоваться упрощенной версией уравнения Беллмана (17.5), которая связывает полезность состояния s (соответствующую стратегии) с по-лезностями его соседних состояний, следующим образом:

Например, предположим, что— это стратегия, показанная на рис. 17.2, а. В таком случае имеет местои т.д., а упрощенные уравнения Беллмана принимают следующий вид:

Важно отметить, что эти уравнения — линейные, поскольку оператор "max" был удален. Для η состояний имеется η линейных уравнений с n неизвестными, которые могут быть решены точно за время с помощью стандартных методов линейной алгебры.